Лекция 10 06.12.2013

Что матрица грамма ММАВ не вырождена даже при линейно зависимых функциях влияния

Значит Ммав оценки можно получить даже в условиях нерегулярных задач оценивания (некорректных) отдельно показано

Иначе говоря: Чтобы спрогнозировать вероятностные свойства процессов в будущем нужно знать свойства этого процесса в настоящем и совсем не обязательно знать всю предысторию рассматриваемого процесса. Это условие может быть сформулировано с помощью корреляционных функций.

Процесс случайный называется стационарным если у него не изменяются характеристики.

Для стационарных случайных процессов принцип марковости запишется вот так:

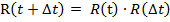
Два марковских процесса:

-Нормальный белый шум

В каждом временном сечении нормальный белый шум имеет распределение Гаусса

, где

Т.е. в любые скольугодно-близкие моменты времени значения процесса некорриелированны. Мощность такого сигнала практически неограничена, т.к. два его соседних значения могут отличаться на бесконечно большую величину, а что бы это реализовать нужно иметь бесконечную мощность.

Белый шум нельзя нарисовать. Мы моделируем белый шум на всём слышимом диапазоне и считаем его за бесконечность.

- Винеровский (1894-1964) процесс (шум)

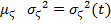
отличительной особенностью Винеровского процесса является то, что его реализации, хотя и непрерывны, но недеференциируемы в любой момент времени. Это свойство позволяет рассматривать нормальный Винеровский процесс как интеграл от нормального белого шума, однако сам интеграл при этом не может быть понимаем в обычном смысле, т.к. изобразить белый шум невозможно даже графически.

Винеровский процесс является процессом с независимыми приращениями, так как его приращения за интервал 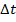полностью не зависят от

Интеграл Итто:

Поиск по сайту: