Статистические свойства МНК оценок

1) Несмещённость оценок: как следует из результатов анализа МНК оценок в линейной задаче МНК-оценки не смещены, если отсутствует систематическая составляющая ошибок измерений

2) Эффективность оценок: Согласно теореме Гаусса-Маркова несмещённая МНК-оценки обладают минимальной дисперсией, т.е. являются эффективными в классе всех линейных несмещённых оценок, другими словами в принципе можно отыскать оценки лучшие чем МНК оценки (при соблюдении исходных допущений относительно условий опыта), но только в нелинейных задачах оценивания.

3) Закон распределения МНК-оценок: т.к. оценки представляют собой величины, наиболее полные заключения о них заключены в вероятностном законе распределения. При произвольном распределении ошибок измерений о Законе распределения оценок вообще говоря однозначно судить невозможно. Однако, в линейной задаче оценивания МНК-оценки получаются в результате линейного преобразования измерительной информации 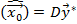, где

В теории вероятностей доказано, что если вектор z распределён по нормальному закону, то его линейное преобразование (в данном случае с помощью матрицы D) даёт нормально распределённый вектор оценок 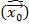. Для других законов распределения z подобного заключения не получено. Однако известно, в соответствие центральной предельной теоремой Ляпунова, при большом числе измерений распределение оценки 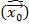является асимптотически нормальным, таким образом, во многих практических ситуациях знания математического ожидания и корреляционной матрицы достаточно для полной характеристики вектора оценок 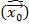, однако, следует иметь ввиду, что для соблюдения выводов центральной предельной теоремы необходимо как минимум два ограничения, чтобы 1) ошибки измерений были попарно независимы и 2) имели примерно одинаковые дисперсии.

Поиск по сайту: