АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод наименьших модулей (МНМ)

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Методические основы
  3. I. Предмет и метод теоретической экономики
  4. II. Метод упреждающего вписывания
  5. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  6. II. Методы непрямого остеосинтеза.
  7. II. Проблема источника и метода познания.
  8. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  9. III. Методологические основы истории
  10. III. Предмет, метод и функции философии.
  11. III. Социологический метод
  12. III. УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО КУРСУ «ИСТОРИЯ ЗАРУБЕЖНОЙ ЛИТЕРАТУРЫ К. XIX – НАЧ. XX В.»

-Закон распределения Лапласа.

Предположим, что относительно ошибок измерений представляемых случайной скалярной величиной h, кроме того что они случайны, аддитивны и обладают дисперсию 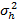. Результат не определён. Неопределенность может быть описана энтропией.

Ограничения:

1) Плотность распределения случайной величины

Что приводит к:

закон распределения случайной величины при условии когда

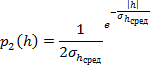
Что является законом Лапласа

Пьер Лаплас 1749-1827 гг.

У метода Лапласа нужно искать отклонение суммы модулей.

Алгоритм метода наименьших модулей.

Будем рассматривать линейную задачу оценивания.

Показатель метода наименьших модулей

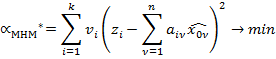
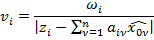
В общем виде алгоритм МНМ выглядит следующим образом:

1)

l:=0 (раньше использовал e)

2) Вычисляется l-ое приближение

Где

3) Решается задача оценивания по МНК, находитсчя очередное приближение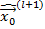

4)

5) () Если выполняется то завершение, если нет то на пункт 2!!!

6) Завершение задачи

Эффективность МНМ

Правила Рао-Крамера, чтобы сравнить оценки получаемые разными методами

дисперсия полученной оценки

точная нижняя граница для дисперсии оценки

 

 

Таблица ассимптотических эффективностей

Метод Закон распределения
Гаусса Лапласа
МНК 1 0,5
МНМ 0,637 1

Крамером было доказано что если оценивается значения скалярного параметра a, предполагается закон распределения ошибок измерений p(h) а фактически реализуется p(h)*, то эффективность применяемого в предположении закона p(h) метода оценивания может быть определена по формуле:

МНМ более устойчив к нарушению условий опыта нежели МНМ. Это свойство называется робастностью алгоритма оценивания. МНМ обладает более тонким эффектом устранения аномальных значений.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)