АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод максимума апостериорной вероятности

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Методические основы
  3. I. Предмет и метод теоретической экономики
  4. II. Метод упреждающего вписывания
  5. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  6. II. Методы непрямого остеосинтеза.
  7. II. Проблема источника и метода познания.
  8. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  9. III. Методологические основы истории
  10. III. Предмет, метод и функции философии.
  11. III. Социологический метод
  12. III. УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО КУРСУ «ИСТОРИЯ ЗАРУБЕЖНОЙ ЛИТЕРАТУРЫ К. XIX – НАЧ. XX В.»

Потенциально необходимая информация для применения методов оценки.

МНК, МНМ, МиниМаксный метод,… – используют минимум информации.

МНР – байесовский подход к получению оценок.

МНР делится на ММП и ММАВ (использование дополнительной информации)

у ММП знание плотности распределения ошибок измерения. h и p(h)

если не гауссовский закон распределения то ещё дополнительные элементы требуются…

Для уточнения орбиты геостационарного КА как раз требуется знание подобной информации.

У ММАВ мы считаем что сам оцениваемый параметр случайный.

Требуется знать:

1) Знание плотности распределения оцениваемого вектора состояния

Общая характеристика ММАВ:

1) Критерии оценивания ММАВ

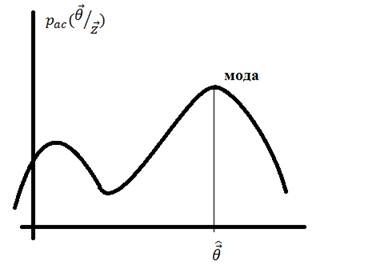
ММАВ исходит из достижения максимума функции плотности апостериорного распределения вероятности, т.е. оценка считается оптимальной по этому критерию при выполнении условий:

1) ММАВ рассматривается как частный случай ММР при простой функции потерь

как обобщение ММП

положительная величина на max не влияет


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |

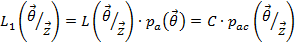
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)