Метод максимального правдоподобия

Общая постановка задачи оценивания данных по МНП.

Ван дер Варден отмечал, что функцию правдоподобия не следует смешивать с плотностью вероятности.

плотность вероятности выборки, при этом множество z есть величина переменная, а множество 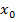фиксированное.

Также её считают функцией правдоподобия, при этом z – фиксированная, а переменная.

О функции правдоподобия, говорят тогда, когда полученные измерения фиксированы.

См. постановку задачи оценивания по методу МНК в линейном случае. При этом по существу мы имеем только несколько мелких отличий:

Здесь мы должны знать плотность распределения ошибок измерения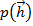

Определение 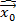называют оценкой максимального правдоподобия, если величина удовлетворяет условию

L( на множестве множестве возможных значений, которые по условию задачи могут быть приписаны параметру .

Смысл этого критерия состоит в том, что если оцениваемому параметру приписать значения 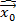то плотность вероятности выборки имеет максимальное значение при фиксированной реализации выборки измерений, полученной в эксперименте. Тем самым полученная выборка становится максимально правдоподобной. Следовательно в принципе максимального правдоподобия отражена идея полного доверия с которым исследователь относится к полученным экспериментальным данным. Алгоритм ММП оценки будет определятся от вида функции правдоподобия, а вид определяется законом изменения ошибки измерений (плотностью вероятности ошибки измерений).

Рассмотрим алгоритм линейного оценивания ММП в предположении нормального закона распределения ошибок измерений.

Сделаем замену

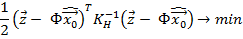
Иногда встречается утверждение, что МНК – частный случай ММП при нормальном гауссовском законе распределения ошибок измерения. На самом деле это не так, по скольку совпадают только алгоритмы оценивания одного из вариантов МНК и одной из реализация ММП. Кроме того МНК и ММП основываются на совершенно различных критериях оценивания: у МНК критерии имеют геометрический смысл, а ММП исходит из критерия вероятностного характера.

Алгоритм линейного оценивания ММП в предположении закона Лапласа распределения ошибок измерений.

Аналогично можно доказать что ММП в нелинейных задачах оценивания приводит к таким же сложным процедурам что МНК и МНМ

Поиск по сайту: