Алгоритмы оценивания МНК

А) Общий вид алгоритма

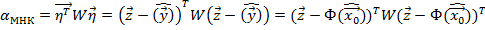
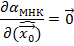
Где 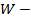является весовой матрицей

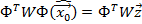
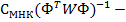Матрица Грама (симметрическая, квадратная), у неё должен быть детерминант не равный 0, т.е. все строки и столбцы не зависимы. Должна быть устойчивой вырожденной, матрица получения МНК оценки называется регулярной.

Б) Рассмотрим различные варианты применения МНК

1) Простой МНК

W=E, где E – единичная матрица. Из (*) следует: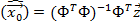

2) Обобщенный метод МНК

Если в прошлом варианте мы считали ошибки измерений по характеру одинаковыми, то здесь считаем их разновеликими и будем учитывать их с весом, который обратнопропорционален

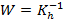
Чем хуже мы меряем (чем больше дисперсия погрешности измерений) тем меньший вес нужно предавать в общей разработке, иначе мы будем ухудшать высокоточные измерения.

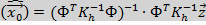
Квантово-оптические средства обладают высокоточными средствами имеют ряд недостатков.

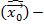вектор состояния сложной динамической системы, в качестве которой может быть движение КА. Начальным моментом времени может быть в момент начального витка измерений.

Характерные точки на орбите КА: восходящий узел, нисходящий узел, апогей перигей, наивысшая точка орбиты, низшая точка орбиты.

Ф – матрица частных производных по оцениваемым параметрам.

В) Точность МНК оценок

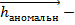обычно выбрасываются, т.к. отличаются от прогнозируемой траектории

Существуют различные методы и критерии для отбраковки аномальных измерений. При запуске при 100 измерениях за 3 минуты может быть до 50% аномальных измерений. Но мы считаем что мы работаем с обработанными данными и аномальных нет.

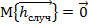
Про систематическую составляющую как правило ничего не известно.

Введём некоторую матрицу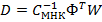

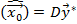
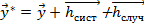
Тогда берём математическое ожидание от оценки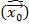

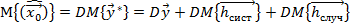
Очевидно 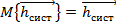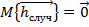- по условию задачи

Тогда: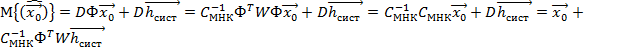

А какой же будет разброс?

Если бы было известно систематическое ожидание можно было бы вычислить реальную оценку.

Оценка характеризуется законом распределения. Если Гаусса, то тут 2 момента: Мат ожидание и дисперсия.

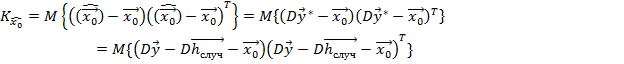
Систематическая составляющая накладывается дополнительно.

Т.к.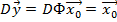

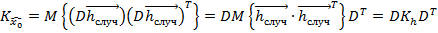
говорим не только о корреляционной матрице в данный момент времени, но и о всех измерениях.

Пусть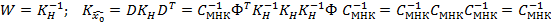

Поиск по сайту: