Граничные условия

Во многих случаях неоднородную среду можно представить в виде совокупности кусочно-непрерывных однородных областей, разделённых бесконечно тонкими границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая» на границах получающиеся решения Для этого проще всего воспользоваться уравнениями Максвелла в интегральной форме. Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно получить следующую связь между компонентами поля в двух областях, примыкающих к границе:

СИ	Словесное выражение
	непрерывность на границе областей тангенциальных компонент напряжённостей электрического поля
	тангенциальные компоненты напряжённости магнитного поля непрерывны только при отсутствии поверхностных токов на границе

где 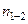— единичный вектор нормали к поверхности, направленный из среды 1 в среду 2 и имеющий размерность, обратную длине, 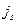— плотность поверхностных свободныхтоков вдоль границы. Аналогичным образом, выбирая область интегрирования в первой паре интегральных уравнений в виде цилиндра бесконечно малой высоты, пересекающего границу раздела так, что его образующие перпендикулярны границе раздела, можно получить:

СИ	Словесное выражение
	Показывают непрерывность нормальной компоненты вектора магнитной индукции

где — поверхностная плотность свободных зарядов

Из уравнения непрерывности можно получить граничное условие для токов:

Частным случаем является граница раздела диэлектрика и идеального проводника. Поскольку идеальный проводник имеет бесконечную проводимость, электрическое поле внутри него равно нулю (иначе оно порождало бы бесконечную плотность тока). Тогда в общем случае переменных полей из уравнений Максвелла следует, что и магнитное поле в проводнике равно нулю. В результате тангенциальная компонента электрического и нормальная магнитного поля на границе с идеальным проводником равны нулю:

Поиск по сайту: