АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Билет № 4

Читайте также:
  1. Билет 1
  2. БИЛЕТ 1
  3. Билет 1
  4. БИЛЕТ 1
  5. Билет 1
  6. Билет 1
  7. Билет 1
  8. Билет 1
  9. Билет 1 Восточные славяне. Расселение, основные занятия, религия. Военная демократия.
  10. Билет 1. Предмет истории как науки: цели и задачи ее изучения
  11. Билет 1.(12)
  12. Билет 10

Теорема о потоке вектора напряженности электрического поля (т.Гаусса). Пример.
Поток вектора напряженности через произвольную замкнутую поверх­ность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0 (ε0 - электрическая постоянная)

 

Применение теоремы Гаусса.
 Напряженность поля, создаваемая бесконечно протяженной однородно заряженной плоскоти с поверхностной плотностью заряда σ.
Поверхностная плотность заряда показывает, какой заряд приходится на единицу площади
1. Линии напряженности перпендикулярны рассматриваемой поверхности и направлены от нее в обе стороны. Построим цилиндр с основанием S, образующая которого параллельна линиям напряженности .

 

 


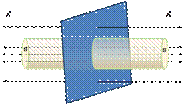
Так как образующая цилиндра параллельна 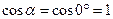, то поток через основание S равен

Поток через боковую поверхность цилиндра равен нулю, т.к. перпендикулярна S cosα= cos90° = 0, следовательно,

2. Напряженность поля, создаваемая двумя параллельными бесконечно протяженными пластинами с поверхностной плотностью зарядов +σ и -σ. Найден поле Е, используя принцип


суперпозиции полей. В области между плоскостями

Слева и справа от плоскостей поля вычитаются, т.к. линии напряженности направлены навстречу друг другу .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)