Билет №6

Потенциал электрического поля. Связь напряжённости и потенциала. Пример.

Электростатический потенциал - скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.

Единицей измерения потенциала в Международной системе единиц (СИ) является вольт

1В = 1Дж/Кл.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

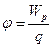
Напряжённость электростатического поля и потенциал связаны соотношением:

или обратно:

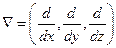
Где 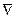— оператор набла.

В прямоугольных декартовых координатах это равенство расписывается как

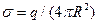Пример: Поле заряда, равномерно распределённого по поверхности сферы радиуса R с поверхностной плоскостью

Система зарядов и, следовательно, само поле центрально-симметричны относительно центра О сферы. Вектор напряжённости поля имеет только радиальную составляющую

,

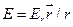где - радиус-вектор, проведённый из центра О сферы в рассматриваемую точку поля; - проекция вектора Е на радиус-вектор, одинаковая во всех точках, равноудалённых от центра О. Поэтому за гауссову поверхность S следует взять сферу радиуса r с центром в точке О. Тогда

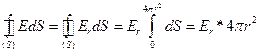
Если r R, то q_охв=q и по теореме Остроградского-Гаусса

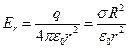
Если r<R, то q_охв=0 и E_r=0, т.е. внутри заряженной сферы поля нет.

Потенциал поля найдём из формулы связи между потенциалом и напряжённостью поля:

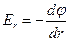
Полагая, что, получаем, что потенциал поля вне сферы равен:

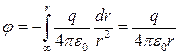
Из этих формул видно, что вне заряженной сферы радиуса R поле такое же, как поле точечного заряда q, находящегося в центре сферы. Внутри заряженной сферы поля нет, так что потенциал всюду одинаков и такой же, как на её поверхности:

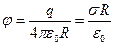
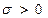
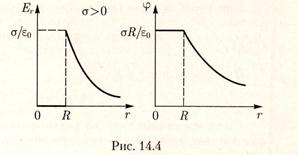
Графики зависимостей E_r и от r для случая, когда

Поиск по сайту: