Билет № 42

Определим проекции вектора Пойнтинга в цилиндрической системе координат, так как вектор напряженности магнитного поля ориентирован по касательной к цилиндрическому проводнику с током, т.е. в цилиндрической системе координат имеет составляющую только, то вектор Пойнтинга не будет иметь такой проекции. При этом Пz=ErHα; Пr=EzHα.

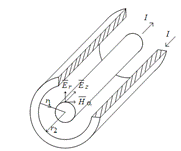
Рис. 18.2. Отрезок коаксиального кабеля

Напряженность электрического поля в диэлектрике определяется зарядом и током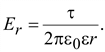

Напряжение между жилами кабеля

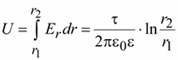
.Следовательно, на поверхности жилы

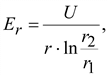
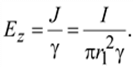
По закону полного тока

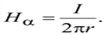
Тогда

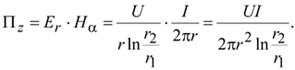
Из формулы видно, что плотность потока энергии имеет наибольшее значение вблизи жилы

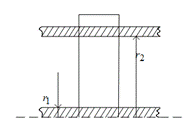
Рис. 18.3. К определению плотности тока энергии

За пределами кабеля магнитного поля нет (H=0).

В пределах оболочки нет радиальной составляющей вектора поля, следовательно, нет потока.

Угловая и радиальная составляющие напряженностей имеются только в кольцевом сечении диэлектрика.

Следовательно, энергия в осевом направлении передается по зазору в кабеле, а проводники служат как направляющие для потока.

Радиальная составляющая вектора Пойнтинга на поверхности жилы

Полагая, что плотность тока энергии на поверхности жилы одинакова, найдем энергию

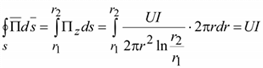
т.к.

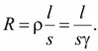
Следовательно, радиальная составляющая вектора Пойнтинга определяет потери энергии в проводнике при протекании по нему тока.

43 вопрос.

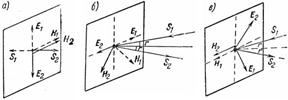
- это среднее по времени от модуля вектора плотности потока энергии:

Для гармонической волны:

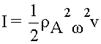При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит.

Для волны, бегущей по оси x:

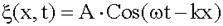
Для волны, бегущей против оси x:

Для простоты мы положили равным нулю значение начальных фаз этих волн. Сумма этих уравнений и дает уравнение стоячей волны:

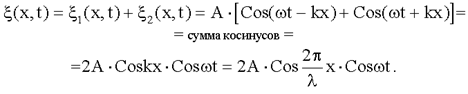
- это модуль выражения, стоящего перед множителем Cosωt, т.е.

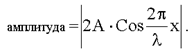
Поверхность, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:

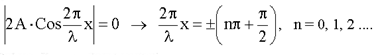
Следовательно, координаты узлов:

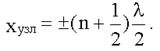
Поверхность, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны.

Для пучностей:

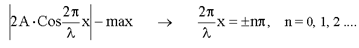
Координаты пучностей:

44 вопрос.

Когерентные волны - это волны, имеющие одинаковые частоты, постоянную раз­ность фаз, а колебания происходят в одной плоскости.Результат суперпозиции волн зависит от того, в каких фазах накладываются друг на друга колебания.Если волны от источников А и Б придут в точку С в одинаковых фазах, то произойдет усиление колебаний; если же — в про­тивоположных фазах, то наблюдается ослабление колебаний.Постоянное во времени явление взаимного усиления и ослаб­ления колебаний в разных точках среды в результате наложения когерентных волн называется интерференцией. В результате в пространстве образуется устойчивая картина чередования об­ластей усиленных и ослабленных колебаний.

Условиe максимума

Для двух когерентных волн можно написать пропорцию: Для двух когерентных волн.

Если колебания вибраторов А и Б совпадают по фазе и име­ют равные амплитуды, то колебания вибраторов А и Б совпадают по фазе и име­ют равные амплитуды, где k=0, 1, 2,...

Тогда Условиe максимума

Если разность хода волн равна целому числу волн (т. е. четному числу по­луволн), то в точке наложения этих волн образуется интерференционный максимум.

Условие минимума

Если волны от вибраторов А и Б придут в точку С в противофазе, то они по­гасят друг друга: А=0. Тогда Если волны от вибраторов А и Б придут в точку С в противофазе, то они по­гасят друг друга. Следовательно, Условие минимума

Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум.

Если разность хода не определяется данными соотношениями, то наблюдается промежуточный результат: 0<А<2х.

Распределение энергии при интерференции.

Наличие минимума в точке С означает: энергия W сюда не поступает.

Наличие максимума в точке С означает: происходит увеличе­ние за счет перераспределения энергии в пространстве. Так как энергия пропорциональна квадрату амплитуды, ТО при увели­чении амплитуды в 2 раза энергия увеличивается в 4 раза. Это означает, что в точку С поступает энергия в 4 раза боль­ше энергии одного вибратора при условии: энергии вибраторов равны.

Стоячие волны

Если раскачивать один конец веревки с правильно подобран­ной частотой (другой ее конец закреплен), то к закрепленному концу побежит непрерывная волна, которая затем отразится с потерей полуволны. Интерференция падающей и отраженной волн приведет к возникновению стоячей волны, которая выгля­дит неподвижной.

Устойчивость стоячей волны удовлетворяет следующему условию: Устойчивость стоячей волны где L—длина веревки; n=1, 2, 3 и т.д.; v—скорость распро­странения волны, которая зависит от натяжения веревки. Стоячие волны возбуждаются в любых телах, способных со­вершать колебания.

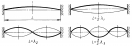Образование стоячих волн является резонансным явлением, которое происходит на резонансных или собственных частотах тела.Точки, где интерференция гасится, называются узлами, а точки, где интерференция усиливается, — пучностями. Помимо поперечных стоячих волн существуют еще и продольные стоячие волны.

Образование стоячих волн является резонансным явлением.

45 вопрос.

Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Эффект назван в честь австрийского физика К. Доплера.

Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны λ) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется — длина волны увеличивается:

где — круговая частота, с которой источник испускает волны, — скорость распространения волн в среде, 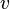— скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).

Частота, регистрируемая неподвижным приёмником

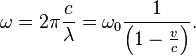
(1)

Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника

(2)

где 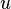— скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).

Подставив вместо в формуле (2) значение частоты 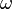из формулы (1), получим формулу для общего случая:

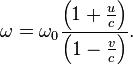
Поиск по сайту: