 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема о циркуляции вектора индукции магнитного поля (т. Стокса). Пример
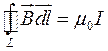Теорема: Циркуляция вектора по произвольному замкнутому контуру L равна произведению µ0 (магнитной постоянной) на алгебраическую сумму токов, охватываемых контуром:
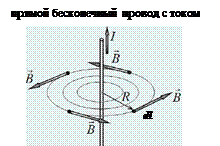Вывод формулы:
 |
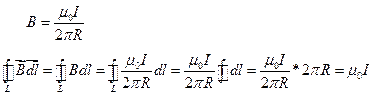
Обобщение: 
Сумма токов, пересекающих контур
понимается в алгебраическом смысле, то есть токи могут быть положительными, так и отрицательными. Сила тока считается положительной, если его направление и направление обхода образуют правый винт.
Так же, как и поток, циркуляция является интегральной (не точечной) характеристикой магнитного поля − из того, что циркуляция по какому-то контуру равна нулю, не следует, что магнитное поле отсутствует (может контур не охватывает ни один ток, или их сумма равна нулю). Токи, не пересекающие контур, так же создают магнитное поле, но циркуляция этого поля по такому контуру равна нулю.
Пример:
Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток (рис. 175). Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный.
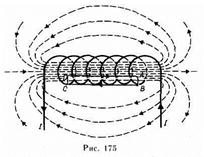На рис. 175 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне него. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.
Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис.175. Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков равна
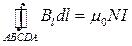
Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CD контур перпендикулярен линиям магнитной индукции и В 1=0. На участке вне соленоида В =0. На участке DA циркуляция вектора В равна Вl (контур совпадает с линией магнитной индукции); следовательно,
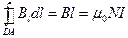
Таким образом, уравнение теоремы о циркуляции в данном случае имеет вид
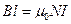
где N − число витков обмотки, которые попали внутрь выбранного контура. Из этого уравнения находим индукцию магнитного поля внутри соленоида.
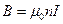
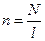
где − число витков обмотки на единицу длины соленоида (плотность намотки).
Из окончательной формулы следует, что поле внутри длинного соленоида является однородным.
Поиск по сайту: