Билет 18

Энергия взаимодействия зарядов.
Потенциальная энергия электростатического взаимодействия двух точечных зарядов 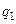и 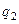, находящихся на расстоянии друг от друга,

рассчитывается по формуле:

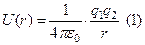
Придадим этой формуле несколько иной вид:

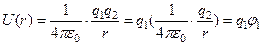
здесь 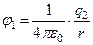потенциал поля, создаваемого вторым зарядом, в точке, где находится первый заряд. Аналогично можно записать
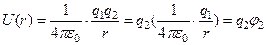где
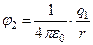потенциал поля, создаваемого первым зарядом, в точке, где находится второй заряд. Теперь перепишем выражение (1) в симметричной форме, легко допускающей обобщение.

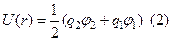
В этой формуле два равных слагаемых, каждое из которых можно трактовать как энергию взаимодействия одного из зарядов с другим, но энергия взаимодействия не «принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды - из-за этого и появляется в формуле множитель 1/2.
Если система состоит из нескольких зарядов 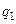, , 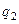… , … 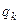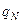( = 1, 2, … 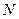), то полная энергия их взаимодействия есть сумма энергий взаимодействий всех пар зарядов. Используя симметричное выражение (2), суммирование по парам зарядов можно заменить на суммирование по самим зарядам, то есть записать:
. - потенциал поля в точке, где находится заряд 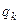, причем поля, создаваемого всеми зарядами, кроме самого заряда .
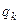Так, если в формуле (3) потенциалы отсчитываются относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу, которую совершит электрическое поле при удалении всех зарядов на бесконечно большие расстояния друг от друга. Для того чтобы разобраться в некоторых нюансах применения формулы (3), рассмотрим пример расчета энергии электростатического взаимодействия.
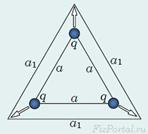
Пусть три одинаковых точечных заряда, величины которых равны между собой 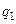= = 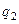= 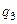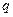, расположены в вершинах правильного треугольника со стороной .

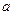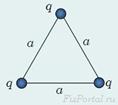
Для расчета энергии взаимодействия этих зарядов заметим, что все заряды равноправны, находятся в одинаковых условиях. В месте расположения одного из зарядов потенциал поля, создаваемого двумя другими зарядами равен:

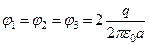
В соответствии с формулой (3) энергия взаимодействия зарядов равна:
.
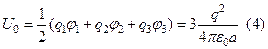Такую работу совершит электрическое поле при удалении всех зарядов на бесконечное расстояние друг от друга.
Если заряды сместятся, так что окажутся в вершинах правильного треугольника со стороной _,

то их энергия окажется равной:

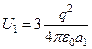
При таком смещении работа электрического поля будет равна уменьшению энергии системы:

Обратите внимание, при эта работа становится в точности равной начальной энергии .
Если из первоначальной системы мы удалим один заряд при неподвижных оставшихся,
то энергия системы станет равной

при этом поле совершит работу

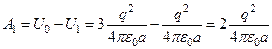
Если теперь удалить еще один заряд, то энергия системы станет равной нулю, при этом поле совершит работу 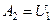. В итоге начальная энергия полностью расходуется на совершение полной работы .

Поиск по сайту: