АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Пример 10. Подстановка выбирается аналогично предыдущему примеру

Читайте также:
  1. X. примерный перечень вопросов к итоговой аттестации
  2. В некоторых странах, например в США, президента заменяет вице-
  3. Вания. Одной из таких областей является, например, регулирова-
  4. Виды знания. Контрпример стандартному пониманию знания
  5. Власть примера. Влияние с помощью харизмы
  6. Внешний долг (внешняя задолженность): пример России
  7. Вопрос 11. Герои романтических поэм М. Ю. Лермонтова (на примере одного произведения).
  8. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  9. Вопрос 8. Герои романтических поэм А. С. Пушкина (на примере одного произведения).
  10. Второй пример абстрактного синтеза
  11. Выбор канала распределения. Факторы, влияющие на выбор канала распределения.. Пример выбора канала распределения.
  12. Выравнивание производства в системы управления производством на примере фирмы «Тойота».

Подстановка выбирается аналогично предыдущему примеру.

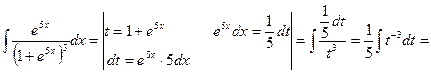
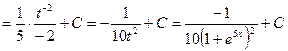
Интеграл из пункта е) вашей контрольной работы берется мето­дом интегрирования «по частям». Этим методом интегрируются не­которые произведения, например, произведения степенной функции на логарифмическую или на показательную, или на тригонометриче­скую, или на обратные тригонометрические функции и др.

Интегрирование «по частям» производится по формуле

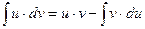
Чтобы воспользоваться этой формулой, следует один множитель в подынтегральном выражении обозначить за «», а оставшийся множитель вместе с принять за «».

Для того, чтобы интеграл в правой части был проще данного ин­теграла, надо правильно выбрать «» и «».

В интегралах, берущихся по частям, обычно логарифмическую и обратные тригонометрические функции принимают за «u». Если по­дынтегральная функция содержит произведение степенной функции на показательную или тригонометрическую, то за «u» принимается степенная функция.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)