АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задачи 11-20

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Ситуационные задачи и тестовые задания.
  3. II. Основные задачи и функции
  4. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  5. II. Цель и задачи государственной политики в области развития инновационной системы
  6. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  7. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  8. Аналитические возможности, задачи и основные направления анализа СНС
  9. БАЛАНС КОММЕРЧЕСКОГО БАНКА, ЦЕЛИ И ЗАДАЧИ ЕГО АНАЛИЗА
  10. Билет 1. Предмет истории как науки: цели и задачи ее изучения
  11. Билет №17. Внутренняя политика Ивана IV Грозного. Задачи, этапы, итоги.
  12. Биофизика – как наука. Практические задачи. Методы исследования

В этих задачах используется определенный интеграл, который вычисляется по формуле Ньютона-Лейбница.

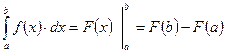
где F(x) - первообразная для f(x), то есть F'(x) = f(x);

a и b - пределы интегрирования, показывающие, как меняется переменная интегрирования х.

Обратите внимание на то, что определенный интеграл - это чис­ло в отличие от неопределенного интеграла, который является множеством функций. Формула Ньютона-Лейбница связывает опреде­ленный и неопределенный интегралы. Чтобы ею воспользоваться, следует взять сначала неопределенный интеграл (вернее, найти лишь одну первообразную, не прибавляя произвольной постоянной), а за­тем вычислить разность значений первообразной в верхнем и нижнем пределах интегрирования.

Например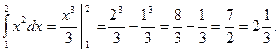

Задача. Вычислить площадь фигуры, ограниченной параболой 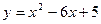и прямой 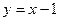. Сделать чертеж.

Решение. Построим параболу и прямую.

Для построения параболы найдем координаты ее вершины и точ­ки пересечения ее с осями координат.

Вершина параболы является точкой экстремума, поэтому для ее отыскания найдем производную и приравняем ее к нулю.

; ; ,

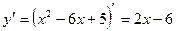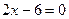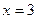Тогда .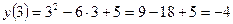

Итак, вершина параболы в точке .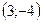

Точки пересечения параболы с осью Ох: , тогда

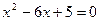, откуда 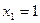; 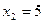, то есть точк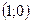и и .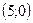

Точка пересечения с осью Оу: 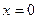, тогда 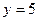; то есть точка .

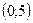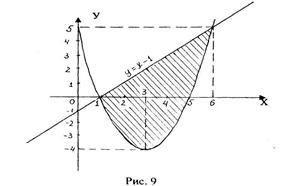
Строим параболу по найденным точкам, замечая, что ветви пара­болы направлены вверх (рис. 9).

Прямую у = х-1 строим по двум точкам: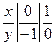

получены точки (0;-1) и (1;0). Заштрихуем плоскую фигуру, ограниченную параболой и пря­мой.

Найдем точки пересечения параболы и прямой, решив систему уравнений:

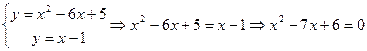
Для отыскания искомой площади воспользуемся формулой

,

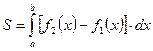где функции f1(x) и f2(x) ограничивают фигуру соответственно снизу и сверху, то есть f2(х) ≥f1 (х) при х Є [а;b].

В нашей задаче f1(x) = x2 -6x + 5;f2(x) = x-l; x Є [l;6].

Поэтому

 

 

 

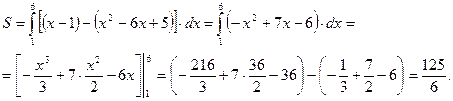
Ответ: Площадь искомой криволинейной трапеции:

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

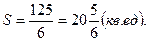
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)