Задачи 41 -50

Исследовать средствами дифференциального исчисления функцию 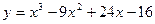и построить ее график.

Решение. Исследование будем проводить по следующей схеме:

1. Область определения функции.

В нашем примере это множество всех действительных чисел, то есть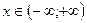

2. Четность и нечетность функции:

Видим, что и 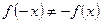, значит, функция

свойствами четности или нечетности не обладает.

Делаем вывод, что график функции не будет симметричен ни относительно оси 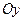, ни относи­тельно начала координат.

3.Периодичность функции.

Данная функция не является периодической, как многочлен.

4.Непрерывность функции.

На всей области определения данная функция является непре­рывной как многочлен.

5.Поведение функции на концах области определения.

Концами области определения являются «-∞» и «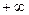», так как .

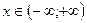Найдем пределы функции при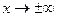

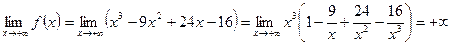
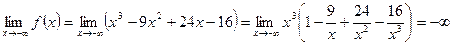
Таким образом, знак бесконечности определяется знаком старшего члена . Это означает, что слева график функции уходит неограни­ченно вниз, а справа - неограниченно вверх

6. Интервалы монотонности и точки экстремумов.

Найдем точки «подозрительные» на экстремум. Согласно необхо­димого условия экстремума: в точках

экстремума производная равна нулю или не существует.

Находим производную: 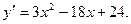. Она существует при лю­бых х. Решим уравнение :

; ;

; .

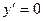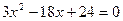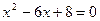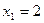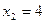Тогда можно записать: .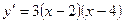

Точки х=2 и х=4 являются критическими. Они делят область оп­ределения на интервалы монотонности функции (интервалы возрас­тания и убывания). Изобразим их на числовой оси (рис.6).

Это интер­валы (-∞; 2);(2;4);(4;+∞).

	+	-	+

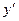
Рис.6

Поведение функции на каждом интервале определяется знаком производной 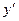: если 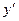<0, то функция убывает, если 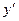>0, то функ­ция 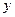возрастает.

Для определения знака производной на каждом интервале доста­точно взять любое значение х из этого интервала и подставить в про­изводную 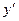= 3(х-2)(х-4).

а) На интервале (-∞; 2), возьмем любое х, например х=0, и под­ставим в производную 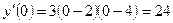.Получили 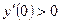, следовательно функция 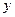возрастает на интервале (-∞; 2).

б) На интервале (2;4) возьмем х=3, подставим в выражение для 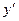, получим 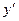(3)=3(3-2)(3-4)<0, следовательно, на интервале(2;4) функ­ция убывает.

в) На интервале (4;+∞) возьмем х=5,видим, что 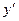(5)= 3(5-2)(5-4)>0, следовательно, на интервале (4;+∞) функция возрастает.

Знаки производной 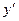проставлены на рис. 6 около каждого ин­тервала.

Замечаем, что при переходе через точку х=2 производная меняет знак, с (+) на (-). Это означает, что в точке х=2 функция имеет мак­симум (на основании достаточного условия существования экстрему­ма). Найдем значение у при х=2:

.

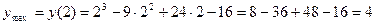Значит, точка максимума (2; 4).

При переходе через точку х=4 производная меняет знак с (-) на (+). Это означает, что при х=4 функция имеет минимум:

.

Точка минимума (4;0).

7. Интервалы выпуклости, вогнутости и точки перегиба. Это исследование проводится с помощью второй производной

Найдем точки, подозрительные на перегиб, используя необходи­мое условие перегиба: в точках перегиба вторая производная либо равна нулю, либо не существует.

Так как , то 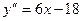существует при любых х. Приравняем вторую производную к нулю и найдем корни уравнения

6х -18=0. Отсюда х=3 - точка, подозрительная на перегиб.

Точка х=3 делит область определения (-∞; +∞) на интервалы: (-∞;3) и (3;+∞) (рис.7).

	-	+
		x

Рис. 7

Определим знаки второй производной на этих интервалах.

Если на интервале >0, то график вогнутый, если <0, то гра­фик выпуклый (на основании достаточного условия выпуклости и вогнутости).

а) На интервале (-∞;3) возьмем, например, х=1, подставим во вторую производную у"=6(х-3), получим 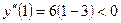, значит, при 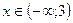график функции выпуклый.

б) На интервале (3;+∞) берем, например, х=5, подставим в ,получим (5) = 6(5-3)>0, значит, при х€(3;+∞) график функции вогнутый.

Знаки проставлены на рис. 7 около каждого интервала.

Так как при переходе через точку х=3 вторая производная у" ме­няет знак, то график меняет выпуклость на вогнутость, то есть при х=3 график функции имеет перегиб.

.

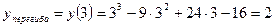Точка перегиба (3;2).

8.Точки пересечения графика с осями координат. С осью Оу: полагаем х=0 и, подставляя это значение в данную функцию у, находим у =-16; получим точку (0;-16). С осью Ох: полагаем у=0, находим х из уравнения

х³-9х²+24х-16=0. (*)

Кубическое уравнение имеет хотя бы один действительный ко­рень, попробуем найти его подбором.

Корни уравнения являются делителями свободного члена 16. Следовательно, попробуем подставлять в уравнение (*) числа ±1; ±2; ±4; ±8; ±16.

При х=1: получаем 1-9+24-16=0, следовательно, х₁=1 является корнем уравнения (*). Тогда многочлен х³-9х²+24х-16 делится на (х-1) без остатка.

После деления в частном получится многочлен второй степени:

_ х³-9х²+24х-16 | х-1.

х³-х² |х²-8х+16

_-8х²+24х-16

- 8х²+8х

_16х-16

16х-16

Каждое слагаемое частного получается делением старшего члена делимого на старший член делителя:х³:х = х² (х² записываем в частное); умножаем (х-1) на х² и вычитаем из делимого. С остатком поступаем аналогично: -8х²:х = -8х (записываем в частное), умножаем (х-1) на (-8х) и вычитаем из остатка и т.д.

Итак, х³-9х²+24х-16 = (х-1)(х²-8х+16). Для отыскания остальных корней х₂ и х₃ решим уравнение х²-8х+16 =0, откуда получим .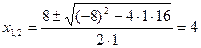

Окончательно: х³-9х²+24х-16 = (х-1)(х-4)².

Уравнение (*) принимает вид: (х-1)(х-4)(х-4)=0, откуда х,=1; х₂=4; х₃=4.

Таким образом, график функции пересекает ось ОХ в точках (1;0) и (4;0).

9. Дополнительные точки. Для более точного построения графика можно найти несколько дополнительных точек. Например, найдем у при х=5:

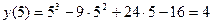. Получим точку К(5;4).

Выпишем результаты исследования функции у = х³-9х²+24х-16.

1. Область определения (-∞; +∞).

2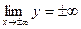

3. Функция возрастает при

Функция убывает при .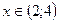

4.Точка max А (2;4), точка min В (4;0).

5. При 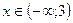- график выпуклый,

при - график вогнутый.

6.Точка перегиба С(3;2)

7.Точки пересечения с осями координат:(1;0), (4;0),(0;-16).

8.Дополнительная точка К (5;4).

Строим график функции (рис.8). Прежде всего построим все ха­рактерные точки, точки пересечения с осями, точки экстремумов, точку перегиба и дополнительные точки.

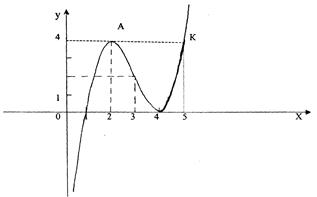
Рис.8

В силу непрерывности функции соединим все построенные точки плавной кривой, продолжив график влево и вправо согласно поведе­нию функции на концах области определения.

Поиск по сайту: