 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачи 1-10
Предварительно ознакомьтесь со следующими вопросами по теме «Аналитическая геометрия на плоскости»:
1. Метод координат на плоскости. Расстояние между двумя точками на плоскости А(х1;у1) и В(х2;у2):

2. Деление отрезка пополам (нахождение середины отрезка):
 ;
; 
3. Угловой коэффициент прямой: k = tgα, где α- угол наклона прямой к оси ОХ, 0 ≤ α < π
4. Уравнение прямой с угловым коэффициентом: у = kx+b.
5. Уравнение прямой, проходящей через заданную точку (хо;уо) в данном направлении (уравнение пучка прямых):
у - уо = k (х - хо).
6. Уравнение прямой, проходящей через две заданные точки (х1;у1) и (х2;у2): 
 ,
, 
7. Общее уравнение прямой Ах + By + С = 0, его частные случаи: Ах+Ву=0, Ах+В=0, Ву+С=0.
8. Угол между двумя прямыми:
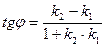
где k1 и k2 - угловые коэффициенты данных прямых.
9. Условие параллельности двух прямых: k1 =k2.
10. Условие перпендикулярности двух прямых:
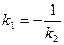
11. Расстояние от точки 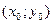 до прямой
до прямой 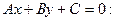
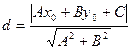
Обратите внимание, что уравнение прямой, в каком бы виде оно ни было записано, является уравнением первой степени.
Задача. Даны вершины треугольника А(2;1), В(-4;4), С(-1,5). Сделать чертеж и найти:
1) длину стороны АВ;
2) внутренний угол А в радианах с точностью до 0,001;
3) уравнение высоты CD, проведенной через вершину С;
4) уравнение медианы BE, проведенной через вершину В;
5) точку пересечения высоты CD и медианы BE;
6) длину высоты, опущенной из вершины С.
Решение. Начнем решение задачи с выполнения чертежа (рис 1).
Построим точки А(2;1), В(-4;4), С(-1;5) в прямоугольной системе координат и, соединив их отрезками прямых, получим треугольник ABC. Проведем высоту CD и медиану BE, уравнения которых нужно найти.

Рис. 1
1. Длину стороны АВ находим как расстояние между двумя точками А(2;1) и В(-4;4) по формуле:
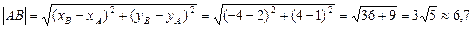 2. При ответе на вопрос пункта 2 (найти внутренний угол) воспользуемся чертежом. Отметим искомый угол А дугой и на ней поставим стрелку, показывающую направление, противоположное движению часовой стрелки. Первой будет та прямая, от которой, направлена стрелка. Так, на рис. 1 первая прямая АС, вторая - АВ.
2. При ответе на вопрос пункта 2 (найти внутренний угол) воспользуемся чертежом. Отметим искомый угол А дугой и на ней поставим стрелку, показывающую направление, противоположное движению часовой стрелки. Первой будет та прямая, от которой, направлена стрелка. Так, на рис. 1 первая прямая АС, вторая - АВ.
Следовательно, в формуле надо положить 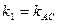 и
и 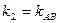
Найдем указанные угловые коэффициенты прямых. Для этого нет необходимости составлять их уравнения, проще воспользоваться формулой, где угловой коэффициент прямой находится по координатам двух ее точек.
Так, в нашем примере:
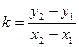
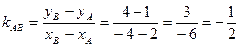
тогда
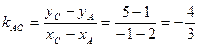
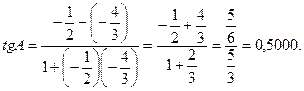
Заметим что tg A > 0, так как угол А - острый.
Из таблицы (например, Брадиса) видно, что такое значение тангенса соответствует углу А=26°34/.
Обратите внимание на то, что ответ следует дать в радианах. Для перевода градусов в радианы можно воспользоваться соответствующими таблицами, либо формулой:
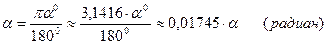
α - угол в градусах.
Итак, в радианах угол  3. Составим уравнение высоты CD. Высота CD перпендикулярна стороне АВ. Угловой коэффициент прямой АВ был найден ранее:
3. Составим уравнение высоты CD. Высота CD перпендикулярна стороне АВ. Угловой коэффициент прямой АВ был найден ранее:
kAВ = -1/2
По условию перпендикулярности двух прямых
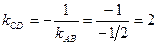
Уравнение высоты СD cоставим по известной точке С (-1;5)
найденному угловому коэффициенту, воспользовавшись урав-
нением  ; пучка прямых:
; пучка прямых:  .
.
Ответ обычно дают в виде уравнения с целыми коэффициентами и с правой частью, равной нулю. Преобразуем полученное уравнение:
 ;
; 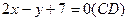
Замечание. Возьмите себе за правило проверять полученные результаты, причем это следует делать не простым повторением проделанных действий, а каким-либо другим способом. Например, полученное уравнение высоты СD проверьте, подставив в него координаты точки С, при этом должно получиться тождество.
Действительно: 2 (- 1) – 5 + 7 = 0.
4. Уравнение медианы ВЕ, проведенной из вершины В, составляется по координатам двух точек В и Е. Координаты точки В известны, а координаты точки Е находим как координаты середины отрезка АС по формулам деления отрезка пополам: 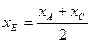 ;
; 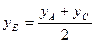
В рассматриваемой задаче
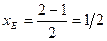 ;
; 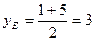
Имея две точки В(-4;4) и Е (1/2;3) Запишем уравнение ВЕ:

а именно:  ;
; 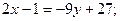
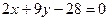 (BE)
(BE)
5. Координаты точки пересечения высоты СD и медианы ВЕ найдем, решив систему уравнений СD и ВЕ:
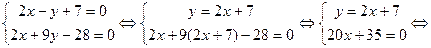
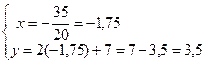
Итак, К(-1,75; 3,5), что соответствует чертежу на рис. 1.
б.Длина высоты СD есть расстояние от вершины С до стороны АВ. Поэтому длину высоты находим по формуле расстояния от точки 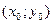 до прямой
до прямой 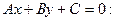

В данной задаче С (-1;5), а уравнение стороны АВ можно составить, используя уравнение пучка прямых:
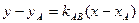 , где
, где  и
и 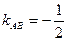
Тогда

Поиск по сайту: