АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задачи 31-40,41-50,51-60

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Ситуационные задачи и тестовые задания.
  3. II. Основные задачи и функции
  4. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  5. II. Цель и задачи государственной политики в области развития инновационной системы
  6. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  7. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  8. Аналитические возможности, задачи и основные направления анализа СНС
  9. БАЛАНС КОММЕРЧЕСКОГО БАНКА, ЦЕЛИ И ЗАДАЧИ ЕГО АНАЛИЗА
  10. Билет 1. Предмет истории как науки: цели и задачи ее изучения
  11. Билет №17. Внутренняя политика Ивана IV Грозного. Задачи, этапы, итоги.
  12. Биофизика – как наука. Практические задачи. Методы исследования

Названные задачи относятся к теме «Дифференциальное исчис­ление и его приложения». Основные вопросы этой темы:

1. Понятие производной, ее геометрический и механический смысл.

2. Правила дифференцирования суммы, разности, произведения, частного и суперпозиции функций.

3. Формулы дифференцирования основных элементарных функ­ций (таблица производных).

4. Дифференциал функции, его геометрический смысл. Примене­ние дифференциала в приближенных вычислениях.

5. Признаки возрастания и убывания для функции одной переменной.

6. Экстремумы функции одной переменной. Необходимое и дос­таточное условия существования экстремумов.

7.Вогнутость и выпуклость графика функции. Признаки выпукло­сти и вогнутости функции.

8.Точки перегиба. Необходимое и достаточное условия перегиба.

9.0бщая схема исследования функции. Построение графика функции.

Таблица производных

Пусть и две функции , , тогда

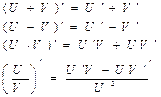
Заметим, что:

а) производная постоянной равна нулю:

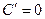
б) постоянный множитель выносится за знак производной: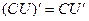

в)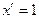


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)