АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Задачи 61-70

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Ситуационные задачи и тестовые задания.
  3. II. Основные задачи и функции
  4. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  5. II. Цель и задачи государственной политики в области развития инновационной системы
  6. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  7. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  8. Аналитические возможности, задачи и основные направления анализа СНС
  9. БАЛАНС КОММЕРЧЕСКОГО БАНКА, ЦЕЛИ И ЗАДАЧИ ЕГО АНАЛИЗА
  10. Билет 1. Предмет истории как науки: цели и задачи ее изучения
  11. Билет №17. Внутренняя политика Ивана IV Грозного. Задачи, этапы, итоги.
  12. Биофизика – как наука. Практические задачи. Методы исследования

Найти полный дифференциал функции двух переменных

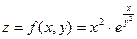
Решение. Полный дифференциал функции двух переменных на­ходим по формуле: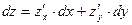

где ; 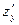--частные производные данной функции z.

Частные производные находим по обычным формулам дифферен­цирования для функции одной переменной, причем находим, счи­тая «у» постоянной величиной; аналогично при отыскании 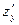счита­ем «х» постоянным:

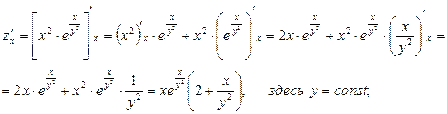
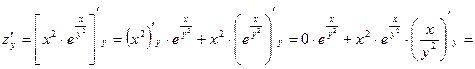
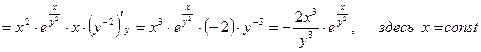
Отсюда полный дифференциал функции:

Задачи 71-80 и 81-90 относятся к теме «Интегральное исчисле­ние». Ознакомьтесь с основными вопросами этой темы:

1. Понятие первообразной и неопределенного интеграла.

2. Основные свойства неопределенного интеграла.

3. Таблица интегралов.

4. Основные методы интегрирования: непосредственное интегри­рование, интегрирование подстановкой, интегрирование по частям.

5. Интегрирование некоторых рациональных дробей.

6. Понятие определенного интеграла и его основные свойства.

7. Формула Ньютона-Лейбница для вычисления определенного интеграла.

8. Замена переменной и интегрирование по частям в определен­ном интеграле.

9. Применение определенного интеграла к вычислению площадей плоских фигур.

Интегрирование есть операция, обратная дифференцированию. ∫f(x)dx = F(x)+C, где F(х)-первообразная для подынтегральной функции f(x), то есть 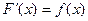, а С - произвольная постоянная. При интегрировании часто используют свойства неопределенного инте­грала:

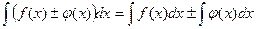
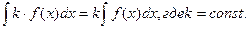
Идея интегрирования заключается в том, чтобы свести данный интеграл к одному из табличных интегралов. Поэтому, приступая к решению задач, ознакомьтесь с таблицей интегралов.

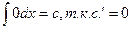
1. 1.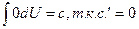
2. 2.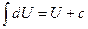
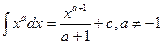
3. 3.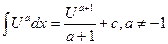
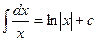
4. 4.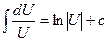
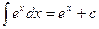
5. 5.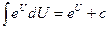
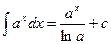
6. 6.
7. 7.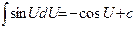
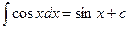
8. 8.
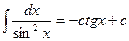
9. 9.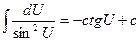
10. 10.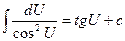
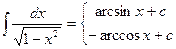
11. 11.
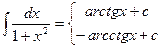
12. 12.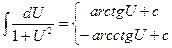
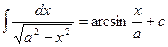
13. 13.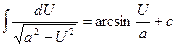
14. 14.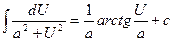
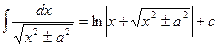
15. 15.
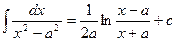
16. 16.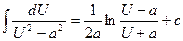

 

Примечание: Формулы интегрирования сохраняют свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е. если

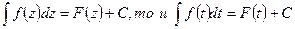
Tаким образом, применение основной таблицы сразу расширяется.

Например


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)