 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задачи 11-20. Предварительно ознакомьтесь со следующими вопросами по теме «Кривые второго порядка»
Предварительно ознакомьтесь со следующими вопросами по теме «Кривые второго порядка»
1. Что называется кривой второго порядка?
2. Канонические уравнения кривых второго порядка. Графики этих кривых:
а) окружность: 
б) эллипс:  ;
;
в) гипербола: 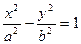 ;
;
г) парабола:  (с осью симметрии Оу),
(с осью симметрии Оу),
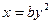 (с осью симметрии Ох).
(с осью симметрии Ох).
З. Параллельный перенос системы координат. Приведение уравнения второго порядка к каноническому виду.
Указанные виды кривых исчерпывают все виды кривых второго порядка (исключая случаи вырождения).
В результате решения задачи вы должны получить одну из названных кривых и построить ее в прямоугольной системе координат.
Задача. Составить уравнение линии, для каждой точки которой отношение расстояний до точки F(5;0) и до прямой  равно
равно  .
.
Решение. Построим в системе координат точку F(5;0) и вертикальную прямую Х=1(рис.2).
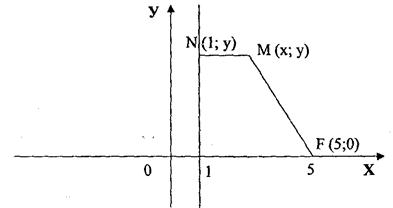
Рис.2.
Пусть М (х,у) - произвольная (текущая) точка искомой линии.
На рис. 2 изображены расстояния от этой точки до заданной точки F, то есть MF, и до заданной прямой: х=1, то есть MN. Обратите внимание, что MN - перпендикуляр к заданной прямой и поэтому точка N имеет (как и точка М) ординату, равную у: N(1;у).
По условию задачи 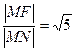
Выразим длины отрезков MF и MN через координаты их концов по формуле расстояния между точками:
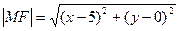 ;
;
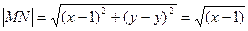
Тогда по условию
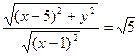

Это и есть уравнение искомой линии. Упростим его, возведя в квадрат обе части уравнения и сделав другие преобразования: 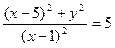 ;
; 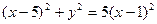 ;
; 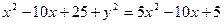 ;
; 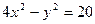
Разделим обе части уравнения на 20: 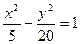
Это каноническое уравнение гиперболы. Из него видно, что действительная полуось гиперболы 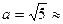 2,25, мнимая полуось
2,25, мнимая полуось  .
.
Центр симметрии гиперболы находится в начале координат. Для построения гиперболы отложим на осях координат в обе стороны от начала координат полуоси гиперболы 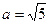 и
и  .
.
Через полученные точки «-а» и «а» на оси Ох и точки «-b» и «b» на оси Оу построим вспомогательный прямоугольник (рис. 3). Проведем диагонали этого прямоугольника, которые являются асимптотами гиперболы: к ним будут неограниченно приближаться ветви гиперболы, Построим кривую, как указано на рис. 3. Задача решена.

Рис. 3
Замечание. Если бы в этой задаче после преобразований вы получили уравнение
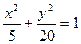
, то оно определяет эллипс, порядок построения которого ясен из рис.4.
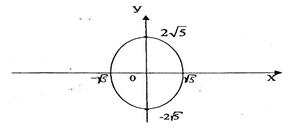
Рис.4
Замечание. Если в задаче вашего варианта после преобразований в уравнении наряду с членами 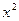 и
и  присутствуют члены, содержащие первые степени
присутствуют члены, содержащие первые степени 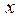 или
или  , то следует выделить полный квадрат (соответственно по
, то следует выделить полный квадрат (соответственно по 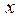 или по
или по  ).
).
Например, в уравнении 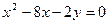 выделим полный квадрат по
выделим полный квадрат по 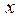 , для чего прибавим и отнимем половину коэффициента при
, для чего прибавим и отнимем половину коэффициента при 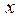 , возведенную в квадрат:
, возведенную в квадрат:
 Обозначим
Обозначим 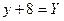 ;
; 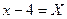 , тогда
, тогда 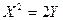 или
или 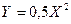 - это каноническое уравнение параболы.
- это каноническое уравнение параболы.
Построим новые оси 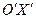 и
и 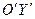 , которые смещены относительно старых осей
, которые смещены относительно старых осей  и
и 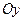 так, что новое начало координат будет находиться в точке
так, что новое начало координат будет находиться в точке  , где и расположена вершина параболы. Ось симметрии параболы
, где и расположена вершина параболы. Ось симметрии параболы 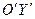 , ветви ее направлены вверх, так как коэффициент при
, ветви ее направлены вверх, так как коэффициент при 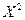 положительный.
положительный.
Полезно найти точки пересечения параболы 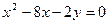 со старыми осями координат
со старыми осями координат  и
и 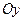 .
.
При 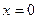 получим
получим 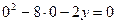 , откуда
, откуда  , таким образом, парабола проходит через точку
, таким образом, парабола проходит через точку  - в старой системе координат.
- в старой системе координат.
 получаем уравнение
получаем уравнение 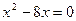 , откуда
, откуда 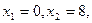 т.е. парабола пересекает ось
т.е. парабола пересекает ось  в точках
в точках  и (8;0) (рис.5)
и (8;0) (рис.5)

Рис.5
Поиск по сайту: