Этап. Формирование системы ограничений. Величины х1 , х2 , х3 следует выбрать так, чтобы стоимость рациона была наименьшей, но при этом в рационе содержалось необходимое количество питательных

Величины х₁, х₂, х₃ следует выбрать так, чтобы стоимость рациона была наименьшей, но при этом в рационе содержалось необходимое количество питательных веществ, т.е. должны выполняться неравенства:

(1)

Так как количество продуктов не может быть отрицательным значением, то появляется условие неотрицательности:

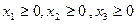
(2)

Таким образом, математическая модель задачи представлена в виде: определить рацион x₁, x₂ , x_3, обеспечивающий минимальное значение функции: L =40x₁+20x₂+30x₃ при наличии ограничений:

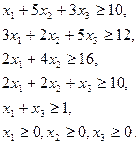
(3)

1.3. Нахождение решения задачи о дневном рационе
средствами Microsoft Excel

Задание 1

Запустите приложение Microsoft Excel (ПускàПрограммыà Microsoft Excel).

Задание 2

Найдите оптимальное решение задачи о дневном рационе:

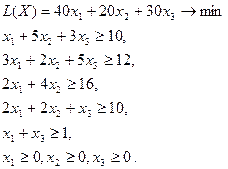
(4)

Для этого выполните следующую последовательность действий:

1. Откройте из папки МАТ_МОД файл lab_1(a), содержащий экранную форму для ввода условия задачи (Рис. 1).

2. Введите исходные данные в экранную форму:

· коэффициенты ЦФ;

· направление целевой функции (min);

· коэффициенты при переменных в ограничениях;

· знаки в ограничениях (>=);

· правые части ограничений.

Напоминаем, для того, чтобы ввести знаки =, >=, <= в соответствующие ячейки, необходимо в ячейку прежде ввести знак апострофа '.

После заполнения форма должна выглядеть следующим образом (Рис. 2).

Рис. 1. Экранная форма для ввода условия задачи

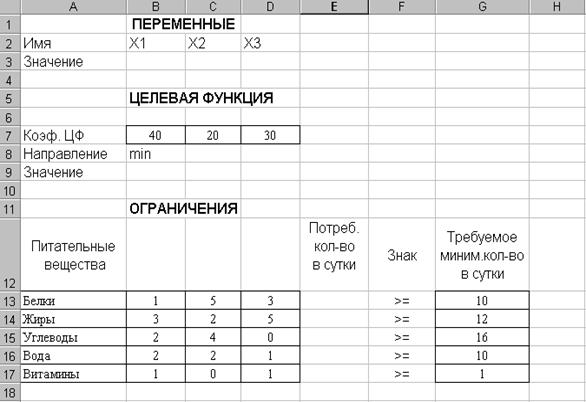
Рис. 2. Ввод исходных данных

3. Введите формулы, описывающие математическую модель задачи, в экранную форму:

· формулу для расчета ЦФ в ячейку;

согласно условию задачи значение ЦФ определяется выражением

,

(5)

поэтому в ячейку B9 необходимо внести формулу

= .

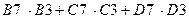(6)

Напоминаем, что данную формулу можно ввести, воспользовавшись функцией =СУММПРОИЗВ(B3:D3;B7:D7), для этого:

· установите курсор в ячейку B9;

· нажав кнопку « », вызовите окно «Мастер функций – шаг 1 из 2»;

· выберите в окне «Категория» категорию «Математические»;

· в окне «Функция» выберитефункцию СУММПРОИЗВ;

· в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение B3:D3, а в строку «Массив 2» – выражение B7:D7;

· нажмите OK.

В экранной форме (Рис. 3) в ячейке B9 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).

· аналогичным образом введите формулы для расчета значений левых частей ограничений (это потребляемое количество в сутки) в ячейки E13, E14, E15, E16, E17 соответственно.

Формулы, описывающие ограничения модели можно увидеть ниже (Таблица 2).

Таблица 2

Поиск по сайту: