АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формулы экранной формы задачи

Читайте также:
  1. BRP открывает новый виток инновационного развития с выпуском платформы Ski-Doo REV
  2. I Психологические принципы, задачи и функции социальной работы
  3. I. 1.1. Пример разработки модели задачи технического контроля
  4. I. 1.2. Общая постановка задачи линейного программирования
  5. I. 2.1. Графический метод решения задачи ЛП
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  8. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  9. I. Ситуационные задачи и тестовые задания.
  10. I. Цель и задачи дисциплины
  11. I.5.3. Подготовка данных для задачи линейного программирования
  12. I.5.4. Решение задачи линейного программирования
Объект математической модели Выражение в Excel
Формула ЦФ в целевой ячейке B20 =СУММПРОИЗВ(C3:E6;C13:E16)
Ограничения по строкам в ячейках F3 F4 F5 F6 =СУММ(C3:E3) =СУММ(C4:E4) =СУММ(C5:E5) =СУММ(C6:E6)
Ограничения по столбцам в ячейках С8 D8 E8 =СУММ(C3:C6) =СУММ(D3:D6) =СУММ(E3:E6)

В экранной форме (Рис. 21) в ячейках F3, F4, F5, F6, C8, D8, E8, B20 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).

6. Осуществите поиск решения задачи, для этого:

· зайдите в меню Сервис à Поиск решения;

· в поле «Установить целевую ячейку» укажите целевую ячейку $B$20;

· введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по кнопке «минимальному значению»;

· укажите диапазон изменения ячеек, для этого в окне в поле «Изменяя ячейки» впишите адреса $C$3:$E$6;

· внесите ограничения, накладываемые на условие задачи (Рис. 22);

· запустите «Поиск решения», нажав на кнопку «Выполнить».

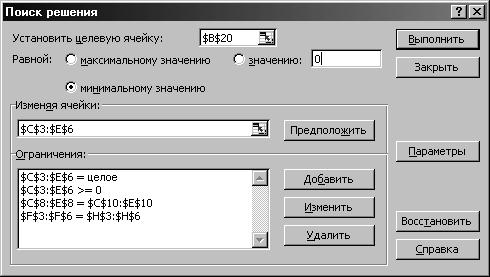
Рис. 22. Ограничения и граничные условия задачи

7. Проанализируйте полученный результат (Рис. 26).

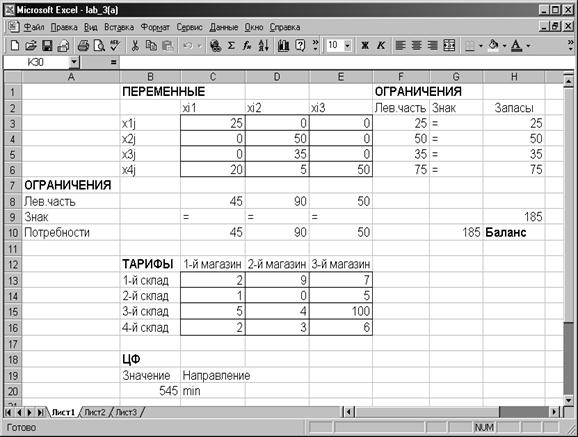
Рис. 23. Решение транспортной задачи

Вывод: c 1-го склада в первый магазин надо перевезти 25 шт. товара, cо 2-го склада во второй магазин надо перевезти 50 шт. товара, c 3-го склада во второй магазин надо перевезти 35 шт. товара, c 4-го склада в первый магазин 20 шт., во второй магазин - 5 шт., в третий магазин – 50 шт. товара, общая стоимость перевозки будет равна 545 рублей.

Задание 12

Сохраните файл в своей папке с именем lab_3(а).

2.2. Решение несбалансированной транспортной задачи

Пусть необходимо организовать оптимальные по транспортным расходам перевозки муки с двух складов в три хлебопекарни. Ежемесячные запасы муки на складах (т), ежемесячные потребности хлебопекарен (т) и транспортные расходы (руб./т) по доставке муки представлены в таблице (Таблица 21). В связи с ремонтными работами временно невозможна перевозка из второго склада в третью хлебопекарню.

Таблица 21

Транспортные расходы по доставке муки (руб./т)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)