Нахождение решение задачи о назначениях средствами Excel

Задание 15

Найдите оптимальный план распределения сотрудников по работам, используя Microsoft Excel, для этого выполните следующие действия:

1. Запустите приложение Microsoft Excel.

2. Откройте из папки МАТ_МОД файл lab_4(а), содержащий экранную форму для ввода условия задачи (Рис. 27).

3. Введите исходные данные в экранную форму.

4. Проверьте выполнение условия баланса, для этого:

· в ячейку L12 введите формулу СУММ(L3:L9), ав ячейку K13 введите формулу СУММ(C13:I13);

· суммы равны, поэтому в ячейке L13 напишите БАЛАНС.

5. Введите зависимости из математической модели (23), (24) в экранную форму, аналогично тому, как Вы это делали, решая транспортные задачи.

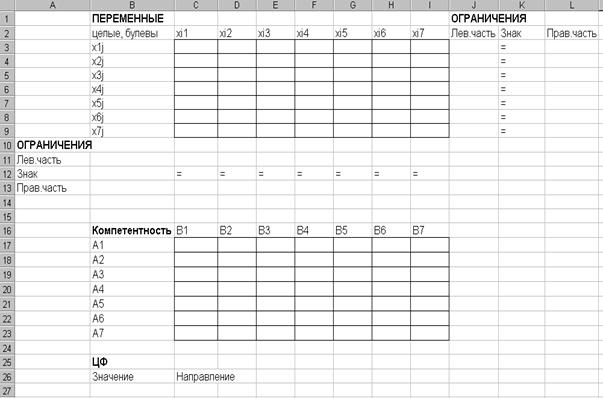
Рис. 27. Экранная форма задачи о назначениях

После выполнения шагов 3-5 Вы должны иметь следующий результат (Рис. 28).

Рис. 28. Экранная форма задачи о назначениях после ввода исходных данных и формул

6. Осуществите поиск решения задачи, заполнив все необходимые поля окна «Поиск решения».

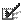Не забудьте указать в окне «Параметры поиска решения» «Линейная модель», а также не забывайте указать, что изменяемые ячейки – это булевы переменные.

7. Проанализируйте полученный результат (Рис. 29).

Рис. 29. Решение задачи о назначениях

Вывод: на первое вакантное место необходимо взять прежнего сотрудника под номером 3, на второе вакантное место – нового сотрудника под номером 2, нового сотрудника под номером 4 взять на место прежнего сотрудника под номером 3, прежних сотрудников под номерами 1 и 2 оставить на своих местах, новым сотрудникам под номерами 1 и 3 – отказать в работе. В этом случае показатель компетентности будет самым высоким.

Напоминаем, что для того, чтобы сбалансировать задачу о назначении, мы ввели фиктивные работы, поэтому значение реальной ЦФ будет меньше значения формальной ЦФ, в которую включена компетентность работников на фиктивных работах.

В нашем примере значение реальной ЦФ будет равно 43-1*2-1*2=39.

Задание 16

Сохраните файл в своей папке с именем lab_4(а).

Задание 17

Откройте файл lab_4(b). Внимательно прочитайте условие задачи о назначении. Введите в предложенную Вам экранную форму необходимые формулы и найдите решение задачи с помощью MS Excel. Убедитесь, что Вы нашли оптимальное решение, для этого сравните полученное Вами решение с тем, что приводится на листе «Результат».

После того, как вся работа будет проделана, пригласите преподавателя и продемонстрируйте ему результат.

3. Резюме

1) Задача о назначениях имеет место при назначении людей на должности или работы, автомашин на маршруты, водителей на машины, при распределении групп по аудиториям, научных тем по научно-исследовательским лабораториям.

2) Задача о назначениях является частным случаем транспортной задачи. Построение модели для задачи о назначениях имеет свои особенности, а вот решение задачи о назначении осуществляется аналогично тому, как решаются транспортные задачи.

Поиск по сайту: