АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение Эйлера

Читайте также:
  1. E) Для фиксированного предложения денег количественное уравнение отражает прямую взаимосвязь между уровнем цен Р и выпуском продукции Y.
  2. IV. УРАВНЕНИЕ ГАМЛЕТА
  3. V2: Волны. Уравнение волны
  4. V2: Уравнение Шредингера
  5. Адиабатический процесс. Уравнение адиабаты (Пуассона). Коэффициент Пуассона.
  6. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  7. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  8. В простом случае обычное дифференциальное уравнение имеет вид
  9. В этом случае уравнение Эйлера принимает вид
  10. Влияние температуры на константу равновесия. Уравнение изобары
  11. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  12. Волна вероятности. Уравнение Шредингера

Исследуем на экстремум функционал: для решения задачи Эйлера. Для начала найдем вариацию функционала по трем этапам (см. вопрос №5). Получим:

. Полученный функционал является линейным. Теперь применим условие экстремума (): 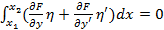- это основная лемма вариационного исчисления, т.е. если мы имеем некий функционал равный нулю при любом 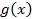, то и . Нужно привести условие экстремума к виду этой леммы, т.е. при 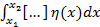Преобразуем выражение (1) и получим:

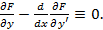
Мы получили дифференциальное уравнение относительно 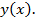Это уравнение Эйлера, которое позволяет решить задачу Эйлера. Интегральные кривые уравнения Эйлера называют экстремалями.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)