Задача синтеза оптимальной системы

Структура системы считается жёстко заданной и требуется найти оптимальные численные значения её параметров, при которых качество системы будет наилучшим с точки зрения выбранного критерия.

Динамический объект может описываться уравнениями:

Динамический объект – объект, движение которого описывается дифференциальными уравнениями, либо записывает систему дифференциальных уравнений в форме Коши:

Движение объекта описывается с помощью решения дифференциальных уравнений.

Решением дифференциального уравнения наз-ся ф-ция, которая при подстановке в дифференциальное уравнение обращает его в тождество.

Линейным дифференциальным уравнением n-ого порядка называется уравнение, линейное относительно неизвестной ф-ции и её производных, имеющие вид:

Линейной системой с постоянными коэффициентами наз-ся линейная система уравнений:

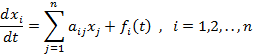
Общая задача математического программирования: поиск наибольших значений функций при ограничениях типа равенств и неравенств.

Функционал – правило отображения ф-ции в число.

Вариация аргумента – приращение аргумента функционала, принадлежащее множеству ф-ций, на котором определён функционал.

Вариация функционала – главная линейная часть приращения функционала.

Принцип оптимальности – конечный участок оптимальной траектории есть оптимальная траектория.

Уравнение Беллмана – уравнение в частных производных для зависимости наименьшего значения критерия оптимальности, зависящего от времени.

Общая постановка задачи линейного программирования: имеется наименьшее значение линейной формы при линейных ограничениях на неотрицательные переменные.

Симплексный метод – метод перехода из одной экстремальной точки в другую соседнюю экстремальную точку, в которой значение критерия предпочтительней.

Уравнение Эйлера: =0

Вариационное исчисление изучает методы, позволяющие находить максимальные и минимальные значения функционалов.

Непрерывная функция: функция f(x) наз-ся непрерывной, если малому изменению х соответствует малое изменение функции f(x).

Линейной функцией наз-ся функция l (x), удовлетворяющая следующим условиям: l (cx)= c l (x), c=const. l (x1+x2)= l (x1)+ l (x2).

Дифференцируемая функция (дифференциал): если приращение ф-ции м.б. представлено в виде , где A(x) не зависит от , а →0 при →0,то ф-ция наз-ся дифференцируемой, а линейная по отношению к часть приращения наз-ся дифференциалом ф-ции и обозначается .

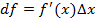
Вариация функционала – главная часть приращения функционала.

Основная лемма вариационного исчисления: если для каждой непрерывной ф-ции y(x):

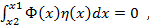где ф-ция Ф(x) непрерывна на отрезке [x0,x1], то Ф(х)=0 на том же отрезке.

Поиск по сайту: