АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод неопределенных множителей Лагранжа при поиске максимальных значений функций

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. FAST (Методика быстрого анализа решения)
  3. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  4. I. 2.1. Графический метод решения задачи ЛП
  5. I. 3.2. Двойственный симплекс-метод.
  6. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  7. I. День максимальных усилий
  8. I. Метод рассмотрения остатков от деления.
  9. I. Методические основы
  10. I. Методические основы оценки эффективности инвестиционных проектов
  11. I. Организационно-методический раздел
  12. I. Предмет и метод теоретической экономики

Методы Оптимизации

 

Общая постановка задачи математического программирования.

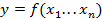
Найти наибольшее и наименьшее значения y при ограничениях:

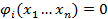, i=1,2,…,k;
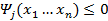, j=1,2,…,l;

Ограничения бывают типа равенств и неравенств.

 

Метод неопределенных множителей Лагранжа при поиске максимальных значений функций.

Найти экстремальные значения y при наличии ограничений типа равенств:


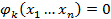
1) Образуем функцию Φ.

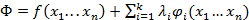от n+k – переменных.

2) Ищем экстремум функции Ф.

3) Пусть M - точка установленного экстремума,

тогда М*= - точка установленного экстремума функции Ф.

2 этапа решения задач:

1) ищется условие оптимальности

2) технический этап – решение уравнений

1-ый способ общий, 2-ой не всегда реализуем.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)