Уравнение Эйлера-Пуассона

Рассмотрим задачу Эйлера-Пуассона. Исследуем на экстремум функционал

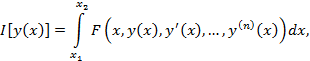
Где функцию F можно считать дифференцируемой 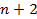раза по всем аргументам, и будем предполагать, что граничные условия имею вид:

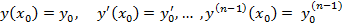
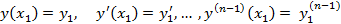
Т.е. в граничных точках заданы не только значения функции, но и ее производных до порядка 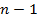включительно. Находим экстремум по трем правилам, и получаем, что на кривой, реализующей экстремум:

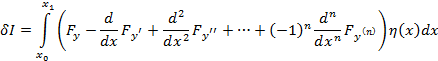
В силу основной леммы вариационного исчисления:

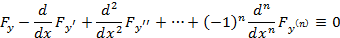
Итак, функция реализующая экстремум исходного функционала должна быть решением уравнения

.

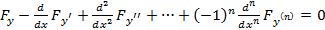Это дифференциальное уравнение порядка 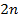носит название Эйлера-Пуассона, а его интегральные кривые называют экстремалями рассматриваемой вариационной задачи. Общее решение этого уравнения состоит из 2 n произвольных постоянных, которые определяются, вообще говоря, из начальных условий.

Поиск по сайту: