АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Симплексный метод

Читайте также:
  1. I. 3.2. Двойственный симплекс-метод.
  2. I.2.3. Табличный симплекс-метод.
  3. А)Равномерный метод.
  4. Абсорбционный метод.
  5. Адсорбционный метод.
  6. Аналитический метод.
  7. Анкетування - це найбільш поширений у соціології метод.
  8. Б) Алгебраический метод.
  9. Бактериологический метод.
  10. Бактериоскопический (микроскопический) метод.
  11. Балансовый метод.
  12. Балансовый метод.

Для решения задач лин. програмир. существует симплексный метод. находясь в одной экстр. т. попеременно в др. так, что значение лин. формы увелич-ся. Движемся по направлению лучших экстр. точек до достижения оптимума…

Задача 1 Множество допустимых значений задано 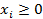N=3

– экстр.т. не явл-ся ()

–явл-ся экстр.т.

–явл-ся экстр.т.

Задача 2 (симплекс. метод)

Задана линейная форма: L= .Найти наим. значение формы L

Симпл. метод перебирает точки, чтобы его реализовать нужно знать хотя бы одну нач. экстр.т.

Для этого формируется доп. задача лин. программирования

Перепишем систему в виде:

пока одна из переменных не обнул-ся, т.е. L до опред. значения (обращаем внимание на переменные с “-” коэфф.) Увеличиваем одну единственную переменную

– пришли в экстр.т.

Можно посчитать значение лин. ф-ции в этой точке. Теперь нулевые координаты

- это свободные переменные. Базовые переменные:

L=-2 Выразим L через своб. перем.:

Для L нужно и , но мы уйдём в “-” область. Т.е. за один шаг симплекс. метода мы завершили алгоритм

Если случай - мн-во решений (

)

Если - задача не имеет решения


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)