Игры без седловых точек

Итак, если матрица игры содержит седловую точку, то ее решение находится по принципу минимакса. Рассмотрим методику решения игры, в платежной матрице которой отсутствует седловая точка. Применение минимаксных стратегий каждым из игроков обеспечивает первому выигрыш не меньше 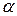, а второму проигрыш не больше 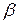. Учитывая, что , естественно для игрока I желание увеличить выигрыш, а для игрока II – уменьшить проигрыш. Поиск такого решения приводит к применению сложной стратегии, состоящей в случайном применении двух и более чистых стратегий с определенными вероятностями. Такая сложная стратегия в теории игр называется смешанной. Смешанные стратегии игроков I и II будем обозначать, соответственно,

и

где 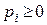, ‑ вероятности применения соответствующих чистых стратегий. Очевидно, должны выполняться условия нормировки для вероятностей

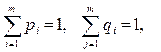
Одна из основных теорем теории игр утверждает, что любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение, возможно, в смешанных стратегиях. Из этой теоремы следует, что каждая конечная игра имеет цену. Обозначим ее так же, как чистую цену игры, через 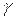. Цена игры 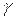– средний выигрыш, приходящийся на одну партию, – всегда удовлетворяет условию 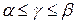, т.е. лежит между нижней (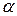) и верхней (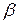) ценами игры. Следовательно, каждый игрок при многократном повторении игры, придерживаясь смешанных стратегий, получает более выгодный для себя результат. Оптимальное решение игры в смешанных стратегиях, так же как и решение в чистых стратегиях, характеризуется тем, что каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет оптимальную смешанную стратегию, так как это ему невыгодно.

Стратегии игроков, входящие в их оптимальные смешанные стратегии, называются активными.

5.5 Использование линейной оптимизации при решении матричных игр

Пусть игра не имеет оптимального решения в чистых стратегиях, т.е. седловая точка отсутствует .

Будем считать, что все элементы платежной матрицы неотрицательны (если это не так, то можно ко всем элементам матрицы добавить некоторое число L, переводящее платежи в область неотрицательных значений - очевидно, при этом цена игры увеличится на L, а решение задачи не изменится). Таким образом, предполагаем, что 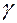>0.

Будем искать решение игры в смешанных стратегиях

;

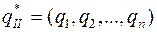
Применение игроком I оптимальной смешанной стратегии гарантирует ему, независимо от поведения игрока II, выигрыш, не меньший цены игры .

Пусть игрок II применяет свою активную чистую j-ю стратегию, а игрок I – свою оптимальную стратегию . Тогда средний выигрыш игрока I будет равен

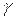Учитывая, что не может быть меньше , запишем условия:

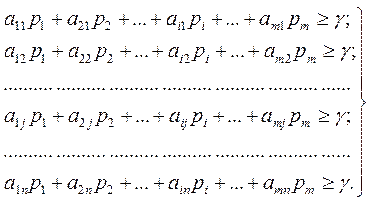(5.4)

Разделив левую и правую части каждого из неравенств (5.4) на цену игры 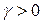, получим

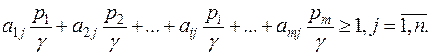(5.5)

При использовании обозначений

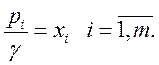(5.6)

неравенства (5.5) примут вид

где, очевидно, все , так как .

Из равенства

и в силу определения (5.6) следует, что переменные () удовлетворяют условию

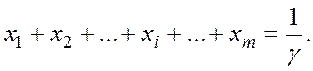
Учитывая, что игрок I стремится максимизировать 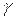, получаем линейную функцию

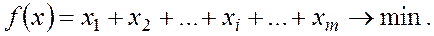(5.8)

Таким образом, задача решения игры свелась к следующей задаче линейной оптимизации: найти неотрицательные значения переменных минимизирующие линейную функцию (5.8) и удовлетворяющие ограничениям (5.7).

Из решения задачи линейной оптимизации легко найти цену игры 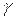и оптимальную стратегию 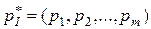игрока I:

В свою очередь, оптимальная стратегия игрока II

может быть найдена из выражения

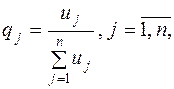
где 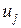- неотрицательные переменные задачи линейной оптимизации

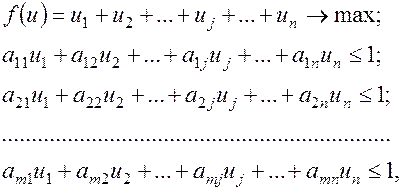
которая является двойственной по отношению к задаче, представленной условиями (5.7) и (5.8).

В этой системе неравенств переменные

Таким образом, оптимальные стратегии

и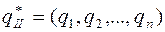

игры с платежной матрицей (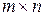) могут быть найдены путем решения симметричной пары двойственных задач линейной оптимизации.

Исходная задача Двойственная задача

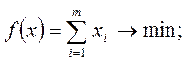
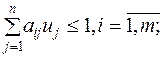
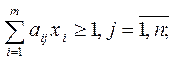
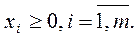
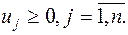
Цена игры и вероятности применения стратегий игроками I и II равны

Поиск по сайту: