 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Автоматизация измерений соответственных точек на стереопаре снимков
Автоматизация измерений соответственных точек на перекрывающихся снимках позволяют в значительной мере уменьшить степень участия в измерениях снимков оператора и, как следствие, значительно повысить производительность выполнения фотограмметрических процессов.
В настоящее время в цифровых фотограмметрических системах в подавляющем большинстве случаев используются методы автоматической идентификации соответственных точек, основанные на сравнении значений одноименных пикселей идентичных по размеру фрагментов цифровых снимков вокруг измеряемых точек (Эти методы иногда называют площадными методами). Одним из таких методов, широко применяющимся в цифровых фотограмметрических системах, является корреляционный метод.
Принцип идентификации соответственных точек на паре снимков корреляционным методом заключается в следующем. На одном из снимков стереопары измеряется точка. Затем вокруг этой точки формируется фрагмент изображения, в виде матрицы, которую будем называть эталонной (рис.1). На втором снимке стереопары в пределах области поиска последовательно формируют аналогичные по размеру матрицы с шагом один пиксель по осям х и у (рис.2).

|
Рис.1
Для каждого положения матрицы формируемой на втором снимке вычисляется коэффициент корреляции R. Положение матрицы, при котором значение коэффициента корреляции является максимальным, соответствует построенной вокруг соответственной точки на втором снимке стереопары. Таким образом, находят координаты соответственной точки на правом снимке. Коэффициент корреляции R изменяется в пределах от 0 до 1.
Коэффициент корреляции вычисляется по формуле:
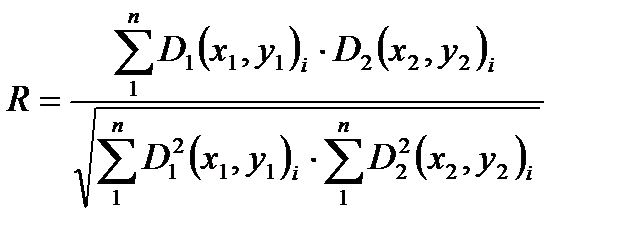 , (.1)
, (.1)
где D1, D2 – оптическиe плотности или яркости пикселей соответственно 1 и 2 цифровых снимков стереопары; i – номер пикселя в матрице; n – количество пикселей в матрице (например, матрицы размерностью 5 х 7, изображенной на рис.2, n =35); x1,y1 и x2,y2 –пиксельные координаты элементов матрицы на снимках 1 и 2 соответственно.
Для компенсации различия в значениях коэффициентов контрастности снимков стереопары, коэффициент корреляции вычисляют по нормализованным значениям оптических плотностей каждого пикселя. Нормализованные значения оптических плотностей каждого пикселя получают путем вычитания из значений плотностей каждого пикселя среднего значения плотностей всех пикселей матрицы.

, где
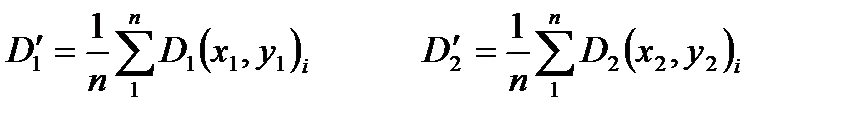 (.2)
(.2)
| Снимок 1 |
| Снимок 2 |
|
|
| Выбраннаяточка (пиксель) |
| Соответственная точка (пиксель) |
Рис
С геометрической точки зрения формулы 1 и 2, по которым вычисляется коэффициент корреляции, являются скалярным произведением двух n -мерных векторов, координатами которых, в нашем случае, являются значения элементов двух сравниваемых матриц, то есть значения оптических плотностей каждого из элементов матриц. Из аналитической геометрии известно, что скалярное произведение двух векторов является косинусом угла между ними. При равенстве координат векторов два вектора совпадают и поэтому значение угла между ними равно 0, а значение косинуса равно 1.
По методике поиска соответственных точек на стереопаре снимков, изложенной выше, можно получать координаты соответственных точек с точностью до одного пикселя. Для получения координат с подпиксельной точностью можно уменьшить шаг перемещения матрицы, например, установить его равным 0.2 пикселя. В этом случае необходимо увеличить исходное цифровое изображения в 2 раза, т.е. один пиксель исходного изображения занимает 2 х 2 пикселей в увеличенном изображении.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAb9uW3cUA AADdAAAADwAAAGRycy9kb3ducmV2LnhtbESPwWrDMBBE74H+g9hCb7GcUJziWgkhpFB6CY2D6XGx traJtTKSart/XwUKOQ4z84YpdrPpxUjOd5YVrJIUBHFtdceNgkv5tnwB4QOyxt4yKfglD7vtw6LA XNuJP2k8h0ZECPscFbQhDLmUvm7JoE/sQBy9b+sMhihdI7XDKcJNL9dpmkmDHceFFgc6tFRfzz9G gTmW4xjKY0PV4WRdRR9fVGZKPT3O+1cQgeZwD/+337WC9Wb1DLc38QnI7R8AAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQBv25bdxQAAAN0AAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " adj="-12682,42675">
| Исходное изображение |
| Увеличенное изображение |
Рис..3
Рис..3
На рис..3 показан пример получения увеличенного изображения в два раза. Если осуществлять поиск соответственных точек на стереопаре снимков по таким изображениям, то точность определения координат будет равна 0.5 пикселя.
Более широко в цифровых фотограмметрических системах применяют другой метод идентификации соответственных точек на стереопаре снимков с подпиксельной точностью. В этом методе, после определения координат центрального пикселя участка (матрицы) изображения по максимуму коэффициента корреляции Rmax, в пределах 2-3 пикселей относительно этого пикселя формируют участки изображения со смещением на один пиксель по оси х и оси у. А затем, определяют для каждого положения участка изображения значение коэффициента корреляции R. Зависимость значений коэффициентов корреляции от значений координат х и у описывают обычно полиномами второй степени (.3).
 . (.3)
. (.3)
На рис..4 графически представлена зависимость (.3) коэффициента корреляции от значения координаты х.
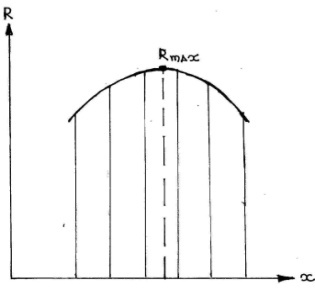
Рис..4
Для определения значений коэффициентов полиномов (.3) по значениям координат х и у и коэффициентов корреляции R для каждого положения участка изображения составляют две системы уравнений поправок (отдельно для осей х и у)

. (.4)
Значения коэффициентов полиномов находят в результате решения полученной системы линейных уравнений поправок по методу наименьших квадратов.
Значения координат соответственной точки на изображении с подпиксельной точностью находят, как максимумы (локальные экстремумы) функций (.3)
Для этого воспользуемся известным положением, что производные функций(.3) в точке локального экстремума Rmax равны нулю, то есть:
 (.5)
(.5)
 (.6)
(.6)
Поиск по сайту: