 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определение элементов внешнего ориентирования снимка по опорным точкам (обратная фотограмметрическая засечка)
Опорной точкой будем называть точку, опознанную на местности и на снимке, координаты которой в системе координат объекта известны.
На рис.1.8.1 опорные точки обозначены треугольниками.
| Y |
| Z |
| X |
| O |
| S |
| x |
| y |
| z |
| o |
Рис. 1.8.1
Для определения элементов внешнего ориентирования снимка воспользуемся уравнениями коллинеарности (1.4.12), которые представим в виде
 (1.8.1)
(1.8.1)
где
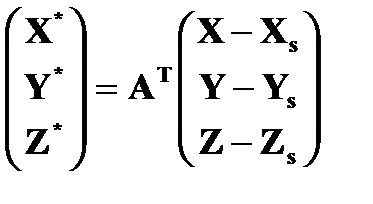
или
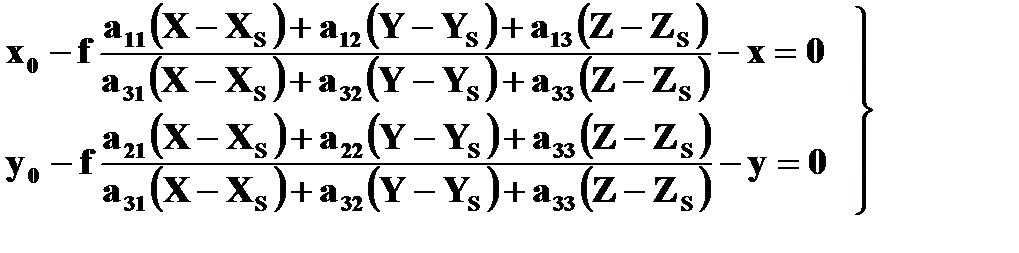 (1.8.2)
(1.8.2)
 Если на снимке измерены координаты изображений опорных точек, то каждая опорная точка позволяет составить 2 уравнения (1.8.2), в которых известны значения координат х,у изображения опорной точки в системе координат снимка Sxyz, координаты опорной точки в системе координат объекта OXYZ и элементы внутреннего ориентирования съемочной системы (снимка) f,xo,yo.
Если на снимке измерены координаты изображений опорных точек, то каждая опорная точка позволяет составить 2 уравнения (1.8.2), в которых известны значения координат х,у изображения опорной точки в системе координат снимка Sxyz, координаты опорной точки в системе координат объекта OXYZ и элементы внутреннего ориентирования съемочной системы (снимка) f,xo,yo.
Неизвестными величинами в уравнениях (1.8.2) являются 6 элементов внешнего ориентирования съемочной системы (снимка) Xs,Ys,Zs,w,a,À.
Следовательно, для определения 6 неизвестных элементов внешнего ориентирования снимка достаточно иметь не менее 3 опорных точек. При этом опорные точки на местности не должны располагаться на одной прямой. Если имеются 3 опорные точки, координаты изображений которых на снимке измерены, можно составить систему из 6 уравнений (1.8.2) с 6 неизвестными. В результате решения этой системы уравнений можно найти значения элементов внешнего ориентирования снимка.
В связи с тем, что уравнения (1.8.2) не линейны, решение системы уравнений непосредственно достаточно сложно, поэтому систему уравнений (1.5.2) решают методом приближений.
Для этого уравнения (1.8.2), приводят к линейному виду, раскладывая их в ряд Тейлора с сохранением членов только первого порядка малости, и переходят к уравнениям поправок.
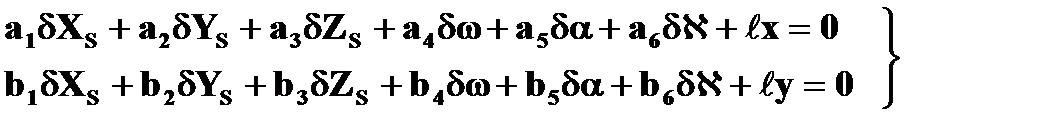 (1.8.3)
(1.8.3)
В линейных уравнениях (1.8.3):
dXs, …,dÀ - поправки к приближенным значениям неизвестных элементов внешнего ориентирования снимка Xs0,…,À0;
ai,bi – частные производные от уравнений (1.8.2) по соответствующим аргументам (например, коэффициент а4 является частной производной от первого уравнения (1.5.2) по аргументу w,то есть  );
);
ℓх, ℓу – свободные члены.
Значения коэффициентов уравнений (1.8.3) ai,bi вычисляются по известным значениям координат точек снимка х,у и местности X,Y,Z, известным значениям элементов внутреннего ориентирования снимка f,x0,y0 и приближенным значениям неизвестных Xso,…,Ào.
Свободные члены ℓх, ℓу вычисляются по формулам (1.8.2) таким же образом.
В результате решения системы уравнений поправок (1.8.3) находят поправки к приближенным значениям неизвестных и вычисляют уточненные значения неизвестных.
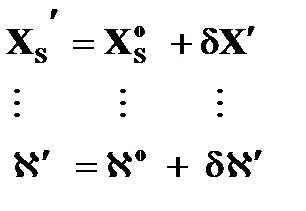
По уточненным значениям неизвестных составляют уравнения поправок и решают полученную систему уравнений.
Решения повторяют до тех пор, пока величины поправок, найденные в результате решения, не станут пренебрежительно малыми.
В случае, если на снимке измерено более трех изображений опорных точек, то для каждой точки составляют уравнения поправок вида:
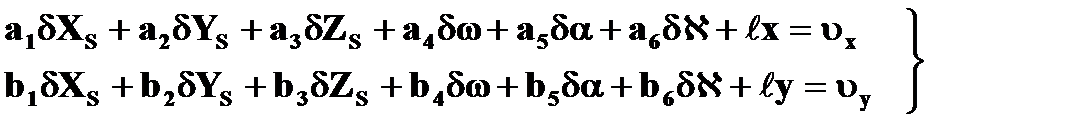 (1.8.4)
(1.8.4)
Решение полученной системы уравнений (1.8.4) производят по методу приближений, по способу наименьших квадратов (под условием VTPV=min). Для этого систему уравнений поправок, которая в матричном виде записывается следующим образом:
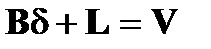 , (1.8.5)
, (1.8.5)
где: B – матрица коэффициентов уравнений поправок (1.8.4) размерностью m x n
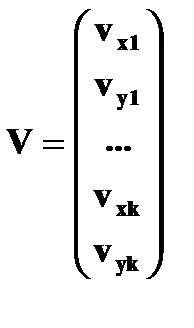
(m – число уравнений, n – число неизвестных); δ – матрица размерностью 1 x n неизвестных поправок к элементам внешнего ориентирования снимка; L –матрица размерностью 1 x m свободных членов; V - матрица размерностью 1 x m поправок в измеренные координаты точек снимка.
В нашем случае m = 2 k, где k – число опорных точек, измеренных на снимке, а n = 6.
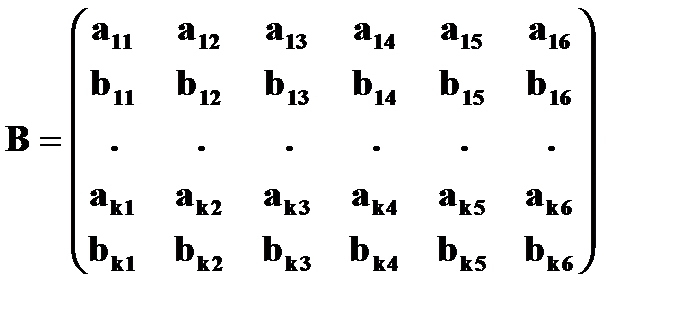 ;
; 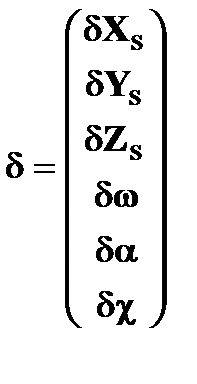 ;
;  ;
; 
Для решения системы линейных уравнений (1.5.5) по способу наименьших квадратов переходят к нормальным уравнениям:
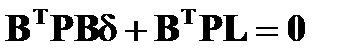
Или
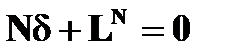 , (1.8.6)
, (1.8.6)
где N - матрица коэффициентов нормальных уравнений размерностью n x n; LN – матрица размерностью 1 x n свободных членов нормальных уравнений; P – диагональная матрица весов измерений:
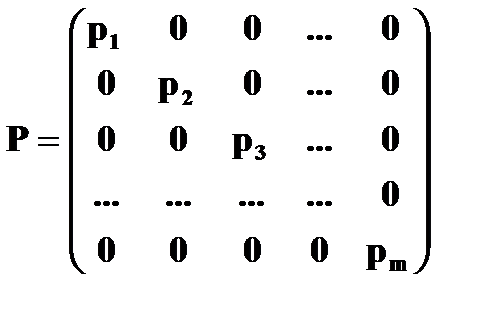
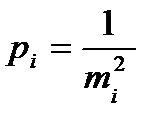
mi – средняя квадратическая ошибка i -го измерения.
В результате решения уравнений (1.8.6) получим:

Или
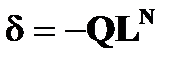 (1.8.7)
(1.8.7)
Здесь Q - обратная матрица коэффициентов нормальных уравнений.
Таким образом, получают поправки ко всем неизвестным элементам внешнего ориентирования снимка. Как уже отмечалось выше, на величины этих поправок уточняют приближенные значения элементов внешнего ориентирования снимка и заново составляют систему уравнений поправок (1.8.5), затем переходят к нормальным уравнениям (1.8.6) и решают их по (1.8.7). Так продолжают до тех пор, пока поправки к неизвестным станут пренебрегаемо малыми величинами.
В результате получают уравненные значения элементов внешнего ориентирования снимка под условием VTPV=min. В последнем приближении выполняют оценку точности определения неизвестных, т.е. вычисляют средние квадратические ошибки неизвестных:
 (1.8.8)
(1.8.8)
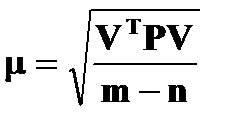 (1.8.9)
(1.8.9)
μ – средняя квадратическая ошибка единицы веса, Qjj – диагональные элементы обратной матрицы; m-n - число избыточных измерений.
Поиск по сайту: