Определение элементов внешнего ориентирования модели по опорным точкам

Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения (2.8.5), которые представим в виде:

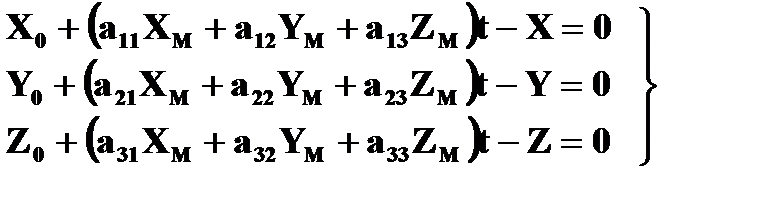(2.9.1)

Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения (2.9.1), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения (2.9.1), а каждая высотная опорная точка (Z) – третье уравнение из выражения (2.9.1).

Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.

В случае, если в полете с помощью спутниковых навигационных систем были определены координаты центров проекций снимков, то они могут быть использованы в качестве опорных точек.

Так как уравнения (2.9.1) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.

(2.9.2)

В уравнении поправок:

a_i, b_i, c_i – частные производные от уравнений (2.9.1) по соответствующим переменным;

ℓ_X, ℓ_Y, ℓ_Z – свободные члены.

Значения коэффициентов уравнений поправок a_i, b_i, c_i вычисляют по известным значениям координат Х_М, Y_M, Z_M и X, Y, Z и приближенным значениям неизвестных. Значения свободных членов ℓ_X, ℓ_Y, ℓ_Z вычисляют таким же образом по формулам (2.9.1).

Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, ее решают по методу наименьших квадратов (под условием V^TPV=min).

Поиск по сайту: