 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Построение и уравнивание маршрутной и блочной фототриангуляции по методу связок
При построении сети фототриангуляции методом связок для каждого изображения точки (определяемой и опорной), измеренного на снимке составляются уравнения коллинеарности:

в которых:
 ;
;
x,y – координаты изображения точки местности, измеренной на снимке;
X,Y,Z – координаты точки местности в системе координат объекта OXYZ;
XS,YS, ZS – координаты центров проекции снимка в системе координат объекта;
А – матрица преобразования координат, элементы a ij которой являются функциями угловых элементов внешнего ориентирования снимка.

Уравнения поправок, соответствующие условным уравнениям (1.5.1),в общем случае, имеют вид:
В случае, если в уравнения 1.5.1 входят измеренные параметры, то из уравнений поправок 1.5.4 исключаются члены соответствующие этим параметрам. Например, в случае, если при съемке были определены угловые и линейные элементы внешнего ориентирования снимка, уравнения поправок имеют вид

Для каждой планово-высотной опорной точки составляются уравнения поправок:

в которых:

X,Y,Z – измеренные координаты опорной точки,
Xo,Yo,Zo – приближенные значения координат опорной точки.
Для плановой опорной точки составляются два первых уравнения из системы уравнений (1.5.5), а для высотной опорной точки третье уравнение.
Если с помощью системы ГНСС были определены координаты центров проекций снимков S, то для каждого центра проекции составляются уравнения поправок:

в которых:

Xs,Ys,Zs – измеренные координаты центров проекции снимков,
XoS, YoS, ZoS – их приближенные значения.
В случае, если при съемке с помощью навигационного комплекса, включающего инерциальную и ГНСС системы, были определены угловые элементы внешнего ориентирования снимков 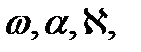 для каждого снимка составляются уравнения поправок:
для каждого снимка составляются уравнения поправок:
 (1.5.7)
(1.5.7)
в которых:

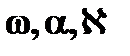 - измеренные значения угловых ЭВО,
- измеренные значения угловых ЭВО,
 - их приближенные значения.
- их приближенные значения.
Полученную таким образом систему уравнений поправок решают методом приближений по методу наименьших квадратов под условием VTPV=min.
В результате решения находят значения элементов ориентирования снимков сети и координаты точек сети в системе координат объекта.
В первом приближении в уравнениях поправок (1.5.5), (1.5.6) и (1.5.7) приближенные значения неизвестных принимаются равными их измеренным значениям.
С геометрической точки зрения сеть фототриангуляции по методу связок строится под условием пересечения соответственных проектирующих лучей связок в точках объекта (рис. 1.5.1):
| S1 |
| L |
| K |
| M |
| N |
| S2 |
| S3 |
| S4 |
| S5 |
| S6 |
| m1 |
| m2 |
| m3 |
| n4 |
| m5 |
| m6 |
| n1 |
| n2 |
| m4 |
| n5 |
| l3 |
| l6 |
| k3 |
| k6 |
Рис. 1.5.1
Общее количество неизвестных, определяемых при построении и уравнивании блочной сети, можно определить по формуле:
 (1.5.8)
(1.5.8)
где n – количество снимков в сети;
k – количество определяемых точек (включая опорные геодезические точки).
Общее количество уравнений поправок можно определить по формуле:
 , (1.5.9)
, (1.5.9)
в которой:
m – общее количество измеренных на снимках точек;
c - количество планово-высотных опорных точек;
i - количество плановых опорных точек;
l – количество высотных опорных точек;
S – количество центров проекций снимков, координаты которых были определены
с помощью системы ГНСС.
Ј – количество снимков, угловые элементы которых были определены.
Рассчитаем величины M и N для блочной сети изображенной на рис. 1.5.2, построенной по двум маршрутам, в каждом из которых 4 снимка, с использованием в качестве опорной информации координаты опорных точек и центров проекции снимков.








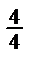







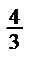



- - главная точка снимка;
- точка сети;
 - планово-высотная точка;
- планово-высотная точка;
- количество точек, измеренных на снимках (в числителе – количество точек, измеренных
на стереокомпараторе или аналитической стереофотограмметрической системе, а в знаменателе – количество точек, измеренных на цифровой фотограмметрической системе).
Для блочной сети, изображенной на рис. 1.5.1, n=8, а k=20, поэтому  .
.
Из рис. 1.5.2 следует, что m=72, если снимки измерялись на стереокомпараторе или аналитическом стереофотограмметрическом приборе, и m=60, если снимки измерялись на цифровой фотограмметрической системе,  , а
, а  . Следовательно,
. Следовательно,  , если снимки измерялись на стереокомпараторе или аналитической стереофотограмметрической системе, и
, если снимки измерялись на стереокомпараторе или аналитической стереофотограмметрической системе, и  , если снимки измерялись на цифровой фотограмметрической системе.
, если снимки измерялись на цифровой фотограмметрической системе.
Поиск по сайту: