 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Внутреннее ориентирование снимка
Для обеспечения возможности определения координат точек в системе координат съемочной системы (снимка) по значению их координат в системе координат цифрового изображения выполняется процесс внутреннего ориентирования снимка. В результате выполнения этого процесса определяются параметры, характеризующие положение и ориентацию системы координат снимка Sxyz в системе координат цифрового изображения ocxcyc, а так же параметры, позволяющие исключить влияние систематической деформации фотоматериала, на котором был получен исходный аналоговый снимок (рис.1.10).
 (xc) (xc)
|
| x |
| y |
| o’ |
 (yc) (yc)
|
 (oc) (oc)
|
Рис.1.10.1
Для определения параметров внутреннего ориентирования снимка измеряют координаты изображений координатных меток снимка в системе координат цифрового изображения oC xC yC.
Выбор метода определения параметров внутреннего ориентирования снимка зависят от методики фотограмметрической калибровки съемочной камеры.
Если в результате фотограмметрической калибровки съемочной
камеры были определены координаты координатных меток в системе координат съемочной камеры (снимка) Sxyz, то для определения координат точек в системе координат снимка по значениям их координат в системе цифрового изображения используют формулы аффиного преобразования координат:
 , (1.10.1)
, (1.10.1)
или в развернутом виде:
 . (1.10.2)
. (1.10.2)
Здесь, ao,a1,a2,bo,b1,b2 – параметры аффинных преобразований; ao,bo – координаты начала системы координат снимка в измерительной системе координат, a1,a2,b1,b2 – параметры, характеризующие ориентацию системы координат снимка в измерительной системе координат, разномасштабность (деформация фотоматериала) вдоль осей системы координат снимка и их неперпендикулярность.
Таким образом, формулы (1.10.1) позволяют не только определить положение и ориентацию системы координат снимка в системе координат цифрового изображения, но и учесть систематические искажения снимка, возникающие из-за деформации фотопленки, на которой был получен снимок.
Параметры аффинного преобразования ai, bi можно определить по координатам 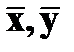 координатных меток снимка, измеренных на цифровом изображении, и значениям координат x,y этих меток в системе координат снимка, полученным при калибровке съемочной камеры.
координатных меток снимка, измеренных на цифровом изображении, и значениям координат x,y этих меток в системе координат снимка, полученным при калибровке съемочной камеры.
Для определения параметров ai,bi для каждой метки, измеренной на цифровом изображении, составляют уравнения:
 . (1.10.2)
. (1.10.2)
Полученную систему уравнений решают по методу наименьших квадратов и определяют в результате решения значения параметров ai, bi. Для их определения необходимо не менее 3 координатных меток, не лежащих на одной прямой.
В практике фотограмметрии возникает обратная задача: определение значений координат точек в измерительной системе координат по координатам этих точек, заданным в системе координат снимка. Такое преобразование координат выполняется по формулам:
 (1.10.3)
(1.10.3)
или
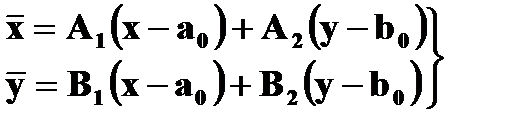 . (1.10.4)
. (1.10.4)
В формулах (1.10.3) и (1.10.4) Ai, Bi – элементы обратной матрицы Р-1.
Для цифровых изображений значение пиксельных координат точек xp,yp определяют по формулам:
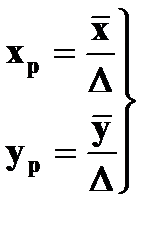 . (1.10.5)
. (1.10.5)
В случае, если при калибровке съемочной камеры определялись калиброванные расстояния между координатными метками Lx, Ly (рис.1.10.2), для определения координат
| Lx |
| Ly |
| φ |
 (xc) (xc)
|
| x |
| y |
| o’ |
 (yc) (yc)
|
 (oc) (oc)
|
Рис.1.10.2
 (1.10.6)
(1.10.6)
В уравнениях (1.10.6) aо, bо – координаты начала системы координат снимка o’ в измерительной системе координат  ; параметры a1, a2 определяют разворот одной системы координат относительно другой(a1 = cosφ, a2 = sinφ); φ – угол поворота (рис.1.10.2); kx, ky – коэффициенты деформации снимка по осям x и y.
; параметры a1, a2 определяют разворот одной системы координат относительно другой(a1 = cosφ, a2 = sinφ); φ – угол поворота (рис.1.10.2); kx, ky – коэффициенты деформации снимка по осям x и y.
Параметры внутреннего ориентирования aо, bо, φ, kx, ky определяют по измерениям координат координатных меток. Параметры aо, bо вычисляют как координаты точки пересечения прямых линий, проведенных через координатные метки 1-2 и 3-4 по формулам:
 (1.10.7)
(1.10.7)
где

Значение угла φ определяют по формуле:
 (1.10.8)
(1.10.8)
Коэффициенты деформации снимка вычисляют по формулам:
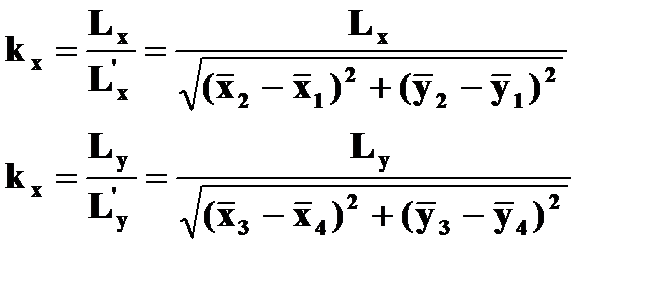 (1.10.9)
(1.10.9)
, в которых:
Lx,Ly – калиброванные значения расстояний между координатными метками (рис.1.7);
L’x,L’y - вычисленные значения расстояний между соответственными координатными метками, на основе измеренных координат этих меток.
Для обратного перехода из системы координат снимка в измерительную систему координат используют формулы:
 (1.10.10)
(1.10.10)
Если отсутствуют данные о значениях расстояний между координатными метками, определение параметров внутреннего ориентирования производится по формулам (1.10.6).
При этом значения коэффициентов деформации принимаются равными kx = ky = 1 получения координат соответствующих точек объекта.
В случае если снимки были получены цифровой камерой, то процесс внутреннего ориентирования снимка не выполняется, так как измерения координат точек снимка выполняются непосредственно в системе координат снимка (рис.1.10.3).
 (o’) (o’)
|
 (x) (x)
|
 (y) (y)
|
Рис.1.10.3
Поиск по сайту: