Негативное (обратное) и позитивное (прямое) изображения

Позитив P получают в случае, когда объект и плоскость проекции расположены по одну сторону от центра проекции S, а негатив N – в в случае когда объект и плоскость проекции расположены по разные стороны от центра проекции S.

Негатив и позитив располагаются симметрично по разные стороны от центра проекции S. Если негатив развернуть на 180^о вокруг оси, проходящей через центр проекции S параллельно плоскостям негатива и позитива, а затем развернуть вокруг оси, лежащей в плоскости позитива и перпендикулярной оси первого разворота, то все точки негатива совпадут с точками позитива. Поэтому при анализе снимка можно рассматривать как негатив, так и позитив.

Элементы снимка.

P – плоскость снимка.

E – предметная (горизонтальная) плоскость.

S – центр проекции (точка фотографирования).

о – главная точка снимка – след пересечения плоскости снимка главным лучом. Главный луч – это луч, проходящий через центр проекции S перпендикулярно плоскости снимка.

So = f – фокусное расстояние съемочной камеры – расстояние от центра проекции до главной точки снимка.

n – точка надира – пересечение отвесной линии, проходящей через центр проекции, с плоскостью снимка.

N – проекция точки надира снимка на плоскость Е.

SN = H – высота фотографирования - высота центра проекции относительно предметной плоскости.

α_о – угол наклона снимка.

on = f tg α_o.

Любая точка местности М на снимке изображается точкой m Прямой линии на местности (K-L) в общем случае соответствует прямая (k-l) на снимке. В частном случае, когда прямая линия на местности (D-F) проходит через центр проекции S, она изображается на снимке в виде точки (df).

Рис. 1.1.4

Точка надира n является точкой схода изображений на снимке вертикальных линий объекта

AB и DM - вертикальные линии на объекте, а ab и dm – их изображения в плоскости снимка P.

Если продолжить изображения вертикальных линий ab и dm, то они пересекутся в точке надира n. Для доказательства этого достаточно провести плоскости через вертикальные линии AB и DM и центр проекции S. Так как эти плоскости вертикальные, то они пересекутся по вертикальной линии SN, проходящей через центр проекции S и точку надира n (которая по определению является точкой пересечения плоскости снимка с отвесной линией, опущенной из центра проекции S). Очевидно, что изображения ab и dm вертикальных линий AB и DM находятся на следах сечения плоскости снимка вертикальными плоскостями SAB и SDM ипересекаются вточке надира n.

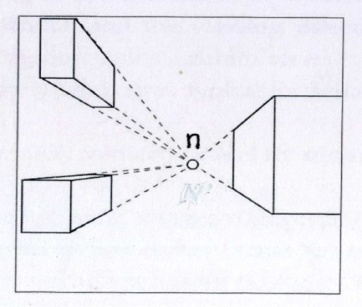
пример изображения на снимке зданий прямоугольной формы.

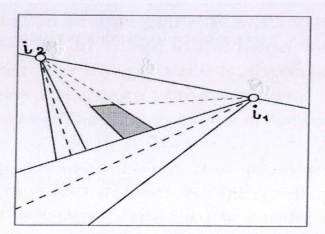
Линия действительного горизонта ii является геометрическим местом точек схода i изображений параллельных прямых линий, расположенных в предметной плоскости E

Построим изображение прямой АВ, расположенной в предметной плоскости Е. Для этого сначала продолжим данную прямую до пересечения с осью перспективы ТТ (линия пересечения плоскости снимка с плоскостью объекта). Полученная таким образом точка Т является одновременно и изображением на снимке. Теперь продолжим линию АВ в обратном направлении до бесконечности. Очевидно, что проектирующий луч, идущий от бесконечно удаленной точки, принадлежащей прямой линии, параллелен этой линии и пересекает снимок в точке схода i, лежащей на линии действительного горизонта. Изображение линии на снимке получают в результате соединения точек i и Т.

Аналогично строят изображения других линий. Если они параллельны между собой в плоскости Е, то из изображения на снимке пересекаются в точке схода i.

пример изображения на перспективном снимке

прямых участков дороги и

прямоугольного объекта

Поиск по сайту: