 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Методы, позволяющие сузить область поиска соответственных точек на смежных снимках
Использование априорной информации о параметрах съемки.
Для сужения области поиска соответственных точек на правом снимке и, как следствие, снижения времени поиска соответственных точек на стереопаре снимков, можно использовать имеющуюся предварительную информацию о параметрах съемки. Например, если известна величина продольного перекрытия между снимками (рис.15а), то соответствующие точки на правом снимке следует искать не по всей площади снимка, а только в пределах этого перекрытия вдоль оси x. Зная возможные пределы изменения поперечных параллаксов ∆q можно ограничить область поиска вдоль оси y (заштрихованная область на рис. 15b). Если известны превышения точек изображенной на снимках стереопары местности, можно вычислить максимальное значение разностей продольных параллаксов ∆p соответственных точек и ограничить область поиска вдоль оси x (заштрихованная область на рис. 15c),
| ∆q |
| ∆q |
| ∆p |
a) b) c)
Рис. 15
Построение пирамиды изображений.
Использование при автоматизации измерения соответственных точек на стереопаре снимков пирамиды изображений является одним из эффективных методов ускорения этого процесса. Пирамида изображений представляет набор изображений получаемых последовательно из исходных изображений путем преобразования и путем пропорционального уменьшения их строк и столбцов. Например, следующее за исходным в пирамиде изображение получают объединением в один пиксель четырех пикселей исходного. (то есть, значение пикселя принимают равным среднему арифметическому из четырех значений пикселей исходного изображения). Таким же образом строятся последующие снимки пирамиды (рис. 16).
Рис.16
Измеренная на исходном изображении точка проектируется на снимок высшего уровня пирамиды и идентифицируется с точностью до одного пикселя корреляционным методом на втором снимке стереопары идентичного уровня пирамиды. Учитывая, что изображение верхнего уровня имеют малые размеры (небольшое число строк и столбцов) поиск соответственной точки на этих снимках выполняется весьма быстро.
Затем процесс идентификации продолжается на стереопаре нижнего уровня. Учитывая, что положение искомой точки известно с точность до пикселя на снимке высшего уровня, область поиска локализуется на снимке в пределах нескольких пикселей, что позволяет произвести быструю идентификацию соответственной точки на снимке. Таким же образом производят поиск на всех снимках пирамид изображений, закончив этот процесс на исходных снимках стереопары.
Использование базисных линий на снимках стереопары.
Известно, что если пара снимков и базис фотографирования взаимно ориентированы, то любая пара соответственных точек находится в базисной плоскости, проходящей через базис фотографирования B и соответственные точки m1 и m2 на стереопаре снимков (рис. 1). Следы сечения снимков стереопары базисными плоскостями называю базисными (или эпиполярными) линиями (линии a-b, и c-d)..
| d |
| S1 |
| M |
| S2 |
| m1 |
| m2 |
| r2 |
| r1 |
| a |
| b |
| c |
| B |
| d |
Рис. 1
Очевидно, что, измерив точку на одном из снимков стереопары, можно провести через эту точку и центры проекции базисную плоскость и построить на другом снимке стереопары базисную линию, на которой будет находиться точка, соответственная измеренной на первом снимке. Для нахождения соответственной точки достаточно провести ее поиск вдоль найденной базисной линии.
Этот поиск выполняется следующим образом. По измеренным на первом снимке стереопары координатам x1,y1, точки, вокруг которой формируется эталонная матрица , известным значениям элементов внутреннего и взаимного ориентирования снимков и заданному значению координаты хc на втором снимке стереопары вычисляется значение координаты уc точки снимка, расположенной на базисной линии (Рис.4). Затем производится формирование матрицы вокруг этой точки и вычисляется коэффициент корреляции R. Задавая значение координаты хc с шагом один пиксель осуществляют поиск соответственной точки на снимке по базисной линии и находят на ней соответственную точку по максимуму коэффициента корреляции R.
Учитывая, что вследствие ошибок определения значений элементов взаимного ориентирования координата уc может быть вычислена с ошибкой, для повышения точности определения координат соответственной точки производят формирование матриц в точках снимка со смещением центральной точки в пределах 1-2 пикселей по оси у.
| S1 |
| S2 |
| m1 |
| m2 |
| rc |
| r1 |
| c |
| B |
Рис. 4
Формулу для вычисления координаты уc получают следующим образом.
Из рис. 4 следует, что векторы B, r1, rc компланарны, так как находятся в одной плоскости. Смешанное произведение этих векторов

В случае использования в качестве элементов взаимного ориентирования параметров a1’, À1’, w2’, a2’, À2’, задавая значения параметров by= bz= w1’=0, в координатной форме смешанное произведение векторов имеет вид:
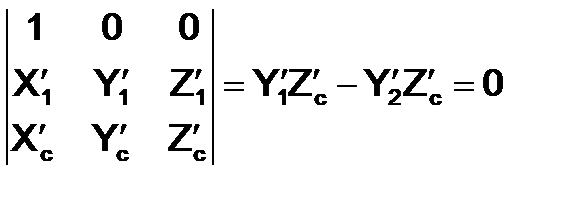 , (.7)
, (.7)
в котором
 , а
, а  .
.
Так как, искомое значение yc входит только в выражения Y’c и Z’с, уравнение (.7) можно представить в виде:
 .
.
В результате простых преобразований. полученного выражения. получим:
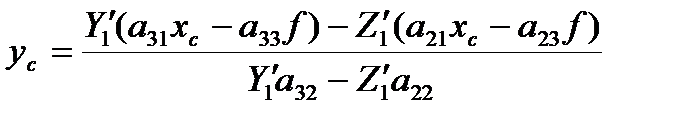 (8)
(8)
Поиск точек на стереопаре снимков идеального случая съемки.
Известно, что на стереопаре снимков идеального случая съемки (угловые элементы внешнего ориентирования снимков этого случая съемки равны нулю, а базис фотографирования параллелен оси Х системы координат объекта) ординаты у соответственных точек равны и, как следствие, значения поперечных параллаксов для всех соответственных точек равны нулю. Очевидно, что при автоматической идентификации точек на стереопаре снимков область поиска ограничивается на снимке линией параллельной оси х снимка, значение координаты у всех точек которой равна значению координаты у центральной точки эталонной матрицы, сформированной на другом снимке стереопары.
Преобразование (трансформирование) исходной стереопары снимков в стереопару снимков идеального случая съемки очень широко применяется в цифровых фотограмметрических системах. Полученные, таким образом, стереопары снимков используются для выполнения работ по построению цифровых моделей рельефа и цифровых моделей объектов, так как при их использовании упрощается выполнение процессов идентификации соответственных точек на стереопаре снимков, и создаются наиболее комфортные условия для стерео наблюдения и измерения снимков.
Для цифрового трансформирования снимков необходимо предварительно выполнить определение элементов взаимного ориентирования снимков. В результате цифрового трансформирования создается стереопара снимков идеального случая съемки в системе координат фотограмметрической модели, ось Х которой параллельна базису фотографирования.
| M |
| m1 |
| m2 |
| S1 |
| S2 |
| m1 |
| m2 |
Рис.5
В реальных случаях оба снимка стереопары имеют, в общем случае, различные значения углов наклона и разворота снимков, базис фотографирования не параллелен оси Х системы координат объекта, а рельеф местности не является горизонтальной плоскостью (Рис..7).

Рис..6
В рассмотренном на Рис..6 случае проекция участка снимка (матрицы) сформированного на первом снимке стереопары на второй снимок стереопары будет иметь вид, представленный на рис..7

|

|
Рис..8
Для случая, представленного на Рис.7 математически строго изображение,представленное на Рис.. 8, может быть получено в результате проективных преобразований эталонной матрицы сформированной на первом снимке. Учитывая, что для идентификации соответственных точек используются весьма малые по размеру фрагменты изображений, математически геометрическое преобразование эталонной матрицы может быть описано более простыми аффинными преобразованиями.

Поиск по сайту: