 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Формулы связи координат точек местности и их изображений на стереопаре снимков (прямая фотограмметрическая засечка)
| Z |
| Y |
| X |
| P |
| P |
| m |
| m |
| r |
| r |
| R |
| R |
| R |
| M |
| S |
| R |
| B |
| M |
| S |
| S |
| • |
| • |
| O |
Рис.2.2.1
На рис.2.2.1 показана стереопара снимков Р1 и Р2 на которых точка местности М изобразилась соответственно в точках m1 и m2. Будем считать, что элементы внутреннего и внешнего ориентирования съемочных систем, с помощью которых были получены снимки, известны.
Выведем формулы связи координат точек местности и координат их изображений на стереопаре снимков.
Из рис.2.2.1 следует, что векторы RM и RS1 определяют соответственно положение точка местности М и центра проекции S1 снимка Р1 относительно начала системы координат объекта OXYZ. Вектор В определяет положение центра проекции S2 снимка Р2 относительно центра проекции S1.
Векторы S1m1 = r1 и S1M = R1 определяют положение точек m1 и М относительно центра проекции S1. Векторы S2m2 = r2 и S2M = R2 определяют положение точек m2 и М относительно центра проекции S2.
Из рис.2.2.1 следует, что
(2.2.1)
Так как векторы R1 и r1 коллинеарны, то
, (2.2.2)
где N – скаляр.
С учетом (2.2.2) выражение (2.2.1) будет иметь вид
(2.2.3)
В координатной форме выражение (2.2.3) будет иметь вид
, (2.2.4)
где X1’,Y1’,Z1’ –координаты вектора r1 в системе координат объекта OXYZ.
Найдем значение N, входящее в выражение (2.2.4). Из рис.2.2.1 следует, что
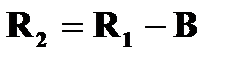
или с учетом (2.2.2)
(2.2.5)
Так как векторы R2 и r2 коллинеарны, то их векторное произведение
(2.2.6)
С учетом (2.2.5) выражение (2.2.6) можно представить в виде
или
(2.2.7)
Выражение (2.2.7) можно представить в виде
или
, (2.2.8)
где:
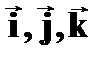- орты, совпадающие с осями координат X,Y,Z системы координат объекта OXYZ;
координаты векторов 
в системе координат объекта OXYZ;
,
где i – номер снимка, а
(2.2.9)
Так как векторы 
и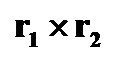 
коллинеарны (потому что векторы 
компланарны), значение N можно найти как отношение их модулей, то есть
(2.2.10)
В координатной форме выражение (2.2.10) с учетом (2.2.8) имеет вид
(2.2.11)
У коллинеарных векторов отношение их координат равно отношению их модулей, поэтому можно записать, что:
(2.2.12)
Таким образом, если известны элементы внутреннего и внешнего ориентирования стереопары снимков и измерены на этих снимках координаты соответственных точек x1,y1 и x2,y2, то сначала надо вычислить по одной из формул (2.2.12) значение скаляра N, а затем по формуле (2.2.4) находятся координаты точки местности X,Y,Z.
Поиск по сайту: