Условие, уравнения и элементы взаимного ориентирования снимков

Рис. 2.5.1

На рис.2.5.1 представлена стереопара снимков Р₁ и Р₂ в положении, которое они занимали в момент фотографирования.

Любая пара соответственных лучей, сформировавших изображения точки объекта на стереопаре снимков, в этом случае пересекается в точке М объекта и лежит в плоскости, проходящей через базис фотографирования (базисной плоскости).

Очевидно, что в этом случае векторы , лежащие в базисной плоскости, компланарны.

Как известно из аналитической геометрии, смешанное произведение компланарных векторов равно нулю.

Таким образом

(2.5.1)

Условие компланарности в координатной форме имеет вид:

(2.5.2)

В уравнении (2.5.2) координаты векторов в системе координат фотограмметрической модели, в общем случае произвольно расположенной и ориентированной.

В дальнейшем эту систему координат будем называть просто системой координат модели.

Условие (2.5.2) связывает между собой только направления векторов и выполняется при любых значениях их модулей. Поэтому значение модуля вектора можно выбрать произвольно. Направление вектора определяется двумя независимыми величинами. В качестве этих величин можно выбрать координаты b_z и b_у вектора 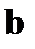, коллинеарного вектору , задав величину координаты b_x произвольно.

В частном случае величину b_x можно выбрать, равной 1.

При этом направление вектора будут определять величины:

и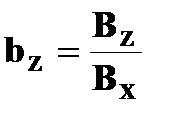

Выражение (2.5.2) в этом случае будет иметь вид:

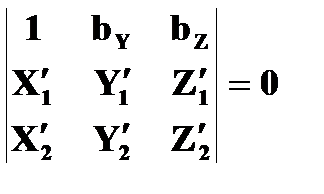(2.5.3)

В уравнении (2.5.3)

,

где i – номер снимка, а А’₁ – ортогональная матрица, элементы a_ij которой являются функциями угловых элементов ориентирования i -го снимка w_i’,a_i’,À_i’ относительно системы координат модели О_МХ_МY_MZ_M.

В выражении (2.5.3), которое является уравнением взаимного ориентирования в общем виде, куда, кроме координат соответственных точек, измеренных на стереопаре снимков, и элементов внутреннего ориентирования, входят 8 параметров b_y, b_z, w₁’, a₁’, À₁’, w₂’, a₂’, À₂’, которые определяют угловую ориентацию базиса фотографирования и стереопары снимков относительно системы координат модели О_МХ_МY_MZ_M.

Причем параметры w₁’ и w₂’ определяют поворот снимков стереопары вокруг оси Х_М, параметры b_z, a₁’, a₂‘ – поворот базиса фотографирования и стереопары снимков вокруг оси Y_M, а параметры b_y, À₁’, À₂ ‘ – поворот базиса фотографирования и стереопары снимков вокруг оси Z_M.

Однако, из этих 8 параметров только 5 определяют взаимную угловую ориентацию базиса фотографирования и стереопары снимков.

Условие (2.5.3) выполняется при любой ориентации системы координат модели О_МХ_МY_MZ_M. Следовательно, ее можно ориентировать таким образом, чтобы 3 из 8 параметров стали равны нулю.

Очевидно, что в общем случае можно сделать равным нулю только один из параметров, входящих в три группы параметров:

– w₁’, w₂’;

– b_z, a₁’, a₂‘;

– b_y, À₁’, À₂’.

Таким образом. в качестве элементов взаимного ориентирования можно выбрать любую комбинацию из восьми параметров b_y, b_z, w₁’, a₁’, À₁’, w₂’, a₂’, À₂’, кроме комбинаций в которые одновременно входят две тройки параметров b_z, a₁’, a₂‘ и b_y, À₁’, À₂’, а также пара параметров w₁’ и w₂’.

Рассмотрим наиболее распространенные системы элементов взаимного ориентирования:

Система a₁’, À₁’, w₂’, a₂’, À₂’. Если принять при этом, что b_y=b_z= w₁’=0, то уравнение (2.5.3) имеет вид:

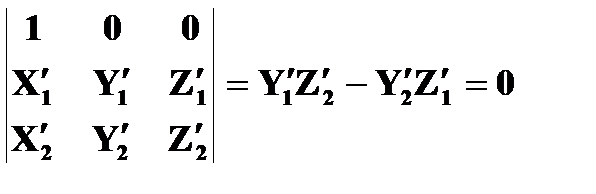(2.5.4)

Система b_y, b_z, w₂’, a₂’, À₂’. Если при этом принять, что w₁’= a₁’= À₁’ =0, то уравнение (2.5.3) будет иметь вид:

, (2.5.5)

так как .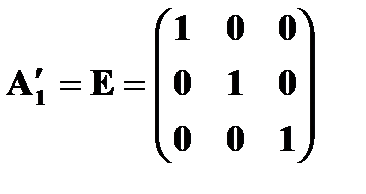

Комментарий. 3 оставшихся из 8 параметров после выбора 5 элементов взаимного ориентирования задают ориентацию системы координат модели О_МХ_МY_MZ_M. Например, выбрав систему элементов взаимного ориентирования b_y, b_z, w₂’, a₂’, À₂’ и приняв, что w₁’= a₁’= À₁’ =0, мы таким образом задаем систему координат модели О_МХ_МY_MZ_M, которой параллельны оси x, y, z системы координат первого снимка стереопары S₁x₁y₁z₁. В общем случае 3 значения можно задавать произвольно.

Поиск по сайту: