Теоретические основы. Давайте попытаемся разработать простую теоретическую модель экспорти­руемых и неэкспортируемых товаров

Давайте попытаемся разработать простую теоретическую модель экспорти­руемых и неэкспортируемых товаров, которую мы назовем TNT-моделью. Вначале обратимся к сфере предложения.

Совокупное предложение в модели TNT

Предположим, что экономика производит и потребляет два вида това­ров — экспортируемые (T) и неэкспортируемые (N). На этой стадии обсуждения примем, что для производства обоих видов товаров требуется толь­ко труд, а производство описывается линейной функцией затрат труда:

где L_T и L_N — затраты труда при производстве соответственно экспортиру­емых и неэкспортируемых товаров, а_T и a_N — коэффициенты, представля­ющие предельную производительность труда при производстве двух типов товаров. Каждая дополнительная единица затрат труда в секторе Т прино­сит дополнительно а_T единиц продукции. Поскольку производственная функция линейна по L_T и L_N, коэффициенты а_T и a_N представляют также и среднюю производительность труда.

Было бы полезно определить границу производственных возможно­стей (PPF) в модели TNT. Допустим, что труд (L), который может быть вложен в секторе Т или секторе N, есть заданная величина. Таким обра­зом, предполагая полную занятость труда, мы имеем:

Воспользовавшись формулами (21.1а) и (21.16), мы можем переписать последнее выражение в терминах выпуска и технологических коэффициен­тов. Поскольку L_T = Q_T/a_T и L_N = Q_N/a_N, мы можем переписать уравне­ние (21.2) следующим образом:

Если выразить Q_N как функцию Q_T (а также L, а_T и a_N, которые мы пред­полагаем фиксированными), то получим:

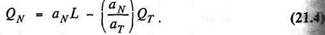
Таким образом, уравнение (21.4) есть уравнение границы производственных возможностей (PPF). Для каждого значения выпуска Q_T она определяет максимальное значение выпуска Q_N для каждой величины Q_T в экономике. Например, если Q_T = 0 (весь труд используется в секторе не экспортируемых товаров), то Q_N = a_NL. Наоборот, Q_T максимально при полной занятости труда в секторе экспортируемых товаров, т.е. Q_T = и Q_N = 0. В общем же случае труд как ресурс будет распределен между двумя секторами.

Граница производственных возможностей показана на рис. 21-1 Объемы производства экспортируемых товаров откладываются по оси Х неэкспортируемых товаров — по оси Y. Если весь труд занят в секторе экспортируемых товаров, тогда производство находится в точке А, где Q_T = a_TL и Q_N = 0. Если, наоборот, весь труд занят в секторе неэкспортиуемых товаров, то производство находится в точке В, где Q_N = a_NL и Q_T = 0. Все остальные точки границы производственных возможностей лежат на отрезке прямой, соединяющей точки А и В (см. рис. 21-1). Любая точка на этой прямой соответствует возможной комбинации производства экспортируемых и неэкспортируемых товаров.

Угол наклона PPF равен отношению уровня цен экспортируемых и неэкспортируемых товаров к относительной цене экспортируемых товаров. Покажем, почему это так. Для каждого вида товара его цена равна затратам труда на производство единицы этого товара (это вытекает из предпо­ложения, что производственная функция линейна по затратам труда). Для выпуска единицы продукции экспортируемого товара необходимо затра­тить 1/а_Т единиц труда. При заработной плате, равной w, стоимость затрат труда на производство единицы Г равна w/a_T. Стоимость затрат труда на производство единицы N равна w/a_N. Таким образом:

Заметим, что это уравнение может быть интерпретировано как условие максимизации прибыли, когда предельный продукт труда должен быть ра­вен заработной плате при производстве этого продукта, измеряемой отно­шением заработной платы к цене выпуска. Таким образом, а_Т = w/P_T и a_N = w/P_N.

Из уравнения (21.5) имеем P_T/P_N = a_N/a_Т . Мы также знаем из урав­нения (21.4), что -(a_N/a_T) равно углу наклона границы производственных возможностей. Следовательно, чем круче наклон PPF, тем выше уровень цен экспортируемых товаров по отношению к уровню цен неэкспортируемых товаров в данной экономике. Этот простой факт имеет важные последствия, которые мы рассмотрим ниже.

В модели TNT принято называть относительную цену экспортируемых товаров реальным обменным курсом. Обозначив через е реальный об­менный курс, получим выражение

Понятно, что угол наклона PPF равен также значению реального обменно­го курса со знаком "минус" (-е). (Отметим здесь существенную семанти­ческую путаницу в принятой экономической терминологии. В моделях с

дифференцированными товарами, рассмотренных в гл. 13 и 14, термин "реальный обменный курс" использовался для обозначения ЕР*/Р. В мо дели TNT тот же самый термин используется для измерения P_T/P_N.)

Поиск по сайту: