ІНДУКТИВНІСТЬ В КОЛІ СИНУСОЇДНОГО СТРУМУ

Рис. 2.11 Коло з індуктивністю L

Розглянемо ідеальну котушку, у якої R= 0. Якщо по котушці протікає змінний струм

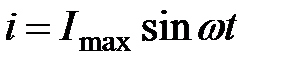, (2.32)

то в ній виникає ЕРС самоіндукції:

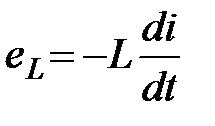. (2.33)

Для того, щоб компенсувати цю ЕРС самоіндукції, необхідно прикласти напругу джерела, яка рівна по величині і протилежна за знаком:

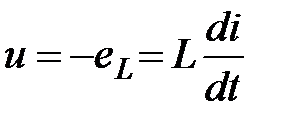. (2.34)

Виконаємо диференціювання синусоїдного струму і при цьому встановимо фазові співвідношення між напругою і струмом, а також введемо поняття індуктивного опору.

. (2.35)

Замінимо косинусоїду на синусоїду:

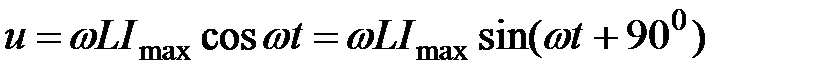(2.36)

Позначимо

(2.37)

і будемо називати його індуктивним опором.

Позначимо і тоді

(2.38)

Порівнявши струм згідно з (2.32) і напругу згідно з (2.38), можна зробити висновок:

у колі з ідеальною індуктивністю напруга випереджає струм на 90⁰, тобто .

Рис. 2.12 Векторна діаграма струму і напруги для ідеальної котушки

На рис. 2.12 показана векторна діаграма стуму і напруги для ідеальної котушки L. Тут же показана ЕРС самоіндукції Е, що заходиться у протифазі з напругою джерела U.

Поиск по сайту: