 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
КОТУШКА ІНДУКТИВНОСТІ У КОЛІ СИНУСОЇДНОЇ НАПУГИ
|
Читайте также: |
Реальна котушка індуктивності має активний (R) і індуктивний (XL) опори.
Рис. 2.15 Коло з реальною котушкою індуктивності
Для схеми на рис. 2.15:
. (2.47)
Тут 
та 
– комплекси падінь напруги на активному та індуктивному опорах котушки. Падіння напруги співпадає за фазою зі струмом, а падіння наруги випереджає струм на 900. На основі (2.47) можна побудувати трикутник напруги (рис. 2.16)
Рис. 2.16 Трикутник напруги для реальної котушки індуктивності
Очевидно кут:
. (2.48)
Рис. 2.17 Трикутник опорів для реальної котушки індуктивності (RL– коло)
Якщо всі сторони трикутника напруги розділити на струм І, то отримаємо трикутник опорів (рис. 2.17).
Із прямокутного трикутника опорів за допомогою формул тригонометрії можна отримати необхідні залежності. Так, модуль повного опору Z – це гіпотенуза прямокутного трикутника:
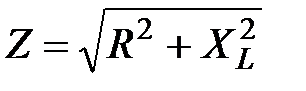(2.49)
Кут
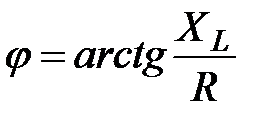, (2.50)
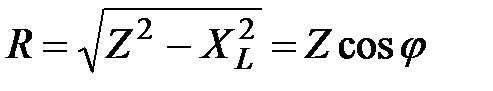(2.51)
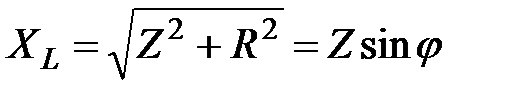(2.52)
Як бачимо із векторної діаграми (рис. 2.16) в RL– колі напруга випереджає струм на кут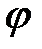 
.
Для реальної котушки індуктивності комплекс опору
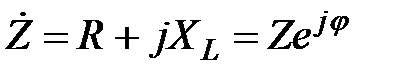(2.53)
2.2.5 ПОСЛІДОВНЕ З’ЄДНАНЯ R, C
Розглянемо коло, в якому на джерело синусоїдного струму послідовно включені R, C.
Рис. 2.18 RC – коло
Для схеми на рис. 2.18:
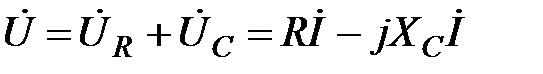. (2.54)
Тут та 
– комплекси падінь напруги на активному та ємнісному опорах котушки. Падіння напруги співпадає за фазою зі струмом, а падіння наруги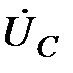 
відстає від струму на 900. На основі (2.54) можна побудувати трикутник напруги (рис. 2.19)
Рис. 2.19 Трикутник напруги для RC – кола
Очевидно кут
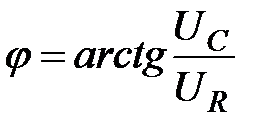. (2.55)
Рис. 2.20 Трикутник опорів для RС– кола
Якщо всі сторони трикутника напруги розділити на струм І, то отримаємо трикутник опорів (рис. 2.20).
Модуль повного опору Z:
. (2.56)
Кут
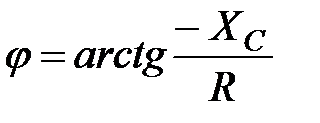, (2.57)
, (2.58)
. (2.59)
Як бачимо із векторної діаграми (рис. 2.19) в RС – колі напруга відстає від струму на кут .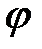
Для RС – кола комплекс опору
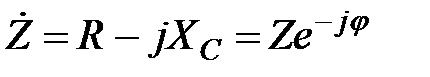. (2.60)
2.2.6 ПОСЛІДОВНЕ ЗЄДНАННЯ R, L, С
Розглянемо схему, в якій послідовно включені резистор з опором R, котушка індуктивності з опорами 
та 
, конденсатор з опором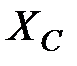 
(рис. 2.21).
Рис. 2.21 RLC – коло
Для цієї схеми:
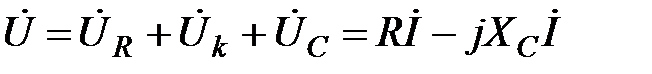(2.61)
Тут потрібно брати 
– падіння напруги на котушці, а не на індуктивності, бо котушка має не тільки індуктивний опір, а й активний опір.
Тому
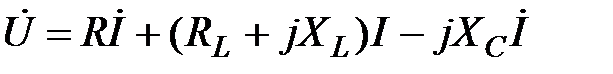(2.62)
Якщо в RLC – колі 
, то коло носить індуктивний характер. Якщо в RLC – колі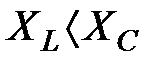 
, то коло носить ємнісний характер.
Модуль повного опору Z:
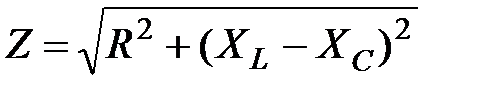. (2.63)
Кут
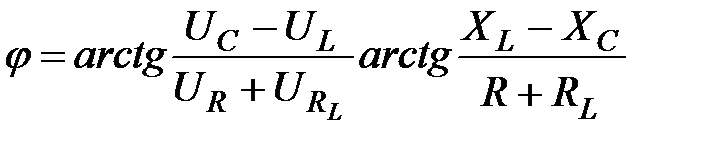, (2.64)
Для RLС – кола комплекс опору
. (2.65)
Питання для самоперевірки знань
1. Зсув фаз у колі з активним опором
2. Хвильова та векторна діаграма для кола активним опором
3. Зсув фаз у колі з індуктивністю
4. Векторна діаграма для кола з індуктивністю
5. Індуктивний опір
6. Зсув фаз у колі з ємністю
7. Векторна діаграма для кола з ємністю
8. Зсув фаз у RL – колі
9. Повний опір для RL – кола
10. Векторна діаграма для RL – кола
11. Трикутник опорів для RL – кола
12. Комплекс опору для RL – кола
13. Зсув фаз у RС – колі
14. Повний опір для RС – кола
15. Векторна діаграма для RС – кола
16. Трикутник опорів для RС– кола
17. Комплекс опору для RС – кола
18. Зсув фаз у RLС – колі
19. Повний опір для RLС – кола
20. Комплекс опору для RLС – кола
Поиск по сайту: