 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Гистограмма. Гистограмма – это инструмент, позволяющий зрительно оценить закон распределения величины разброса данных
|
Читайте также: |
Гистограмма – это инструмент, позволяющий зрительно оценить закон распределения величины разброса данных, а также принять решение о том, на чем следует сфокусировать внимание для целей улучшения процесса [29].
Этапы построения гистограммы:
1. Разработка и заполнение (в процессе наблюдения за контролируемым процессом) бланка для сбора первичных данных – контрольного листка.






 2. Определение максимального (x max) и минимального (x min) значений выборки.
2. Определение максимального (x max) и минимального (x min) значений выборки.
3. Вычисление размаха выборки (R) по формуле:
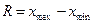 . (1.1)
. (1.1)
4. Определение количества интервалов на гистограмме (n). Число интервалов гистограммы зависит от объема выборки (N), определить его можно с помощью табл. 1.1.
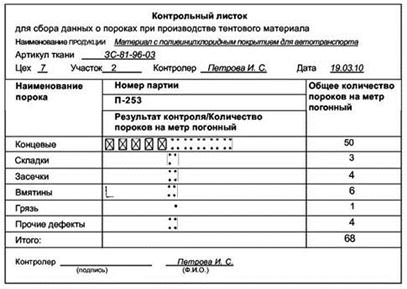
Рис. 1.1. Контрольный листок [29]
|
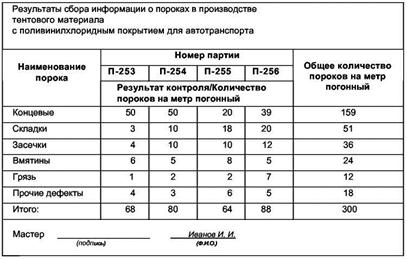
Рис. 1.2. Сводная таблица результатов сбора информации [29]
Таблица 1.1
Определение числа интервалов на гистограмме
| Объем выборки (N) | Число интервалов (n) |
| 23 – 45 | |
| 46 – 90 | |
| 91 – 180 | |
| 181 – 361 | |
| 362 – 723 |
5. Определение размеров интервалов осуществляют так, чтобы размах, включающий максимальное и минимальное значения, делился на интервалы равной ширины. Ширина интервалов (h) определяется по формуле:
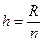 . (1.2)
. (1.2)
6. Определение границ интервалов. Нижней границей первого интервала является минимальное значение выборки, а верхней границей последнего интервала – максимальное.
Первый интервал: [xmin; xmin+ h).
Второй интервал: (xmin+ h; xmin+2  h ] …
h ] …
Последний интервал: [xmin+(n– 1)  h; x max].
h; x max].
7. Определение количества «попаданий» данных в тот или иной интервал (ki).
8. Вычисление относительные частоты «попадания» данных в i -й интервал(fi)
 . (1.3)
. (1.3)
9. Построение графика гистограммы.
На горизонтальную ось необходимо нанести границы интервалов, при этом с обеих сторон (перед первым и после последнего интервалов) следует оставить место для того, чтобы можно было указать верхнюю (USL) и нижнюю (LSL) границы поля допуска. На вертикальной оси наносят относительную частоту. Пользуясь шириной интервалов как основанием, строят прямоугольники, высота каждого из которых равна частоте попадания результатов наблюдений в соответствующий интервал.
Пример гистограммы показа на рис. 1.3.

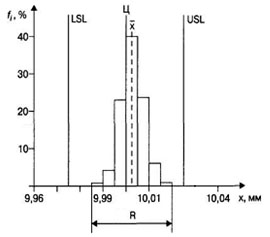
Рис. 1.3. Пример построения гистограммы [29]
На гистограмму необходимо нанести линии, представляющие: среднее арифметическое значение выборки (хср), границы поля допуска (USL и LSL) и середину поля допуска (Ц).
Среднее арифметическое значение хср результатов наблюдений xi определяется по формуле:
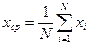 . (1.4)
. (1.4)
Границы поля допуска USL (верхняя) и LSL (нижняя) определяются согласно требованиям стандартов к качеству продукции.
Середина поля допуска или целевое значение (Ц) определяется по формуле:
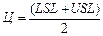 . (1.5)
. (1.5)
Вычисление основных характеристик качества
процесса по гистограмме
Для оценки качества процесса по гистограмме необходимо рассчитать следующие значения:
1. Индекс пригодности процесса удовлетворять технический допуск без учета положения среднего значения (Pp). Определяется по формуле:
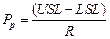 . (1.6)
. (1.6)
Если Pp ≥ 1, то ширина гистограммы укладывается в пределах ширины поля допуска, и процесс является управляемым (точнее говоря, имеется возможность осуществить процесс так, что 99,73 % изделий будут попадать в пределы поля допуска). Если Pp < 1, то процесс является неуправляемым, так как размеры части изделий неизбежно будут выходить за пределы поля допуска.
Большинство российских заводов работают при значениях Pp ≈ 0,95... 1,3, а японским специалистам по управлению качеством продукции во многих случаях удается поддерживать на своих предприятиях значения индекса пригодности процессов Pp ≈ 1,5... 4,0, что позволяет ограничить дефектность продукции единицами бракованных изделий на миллион выпускаемых изделий [29].
2. Показатель настроенности процесса на целевое значение (k). Определяется по формуле:
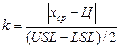 . (1.7)
. (1.7)
3. Индекс пригодности процесса удовлетворять технический допуск с учетом положения среднего значения (Ppk) определяется по формуле:
 . (1.8)
. (1.8)
Для повышения качества процесса (уменьшения уровня дефектности) необходимо обеспечить высокое значение индекса Pp и низкое значение показателя k.
Поиск по сайту: