 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Особенности характеристик линий передач
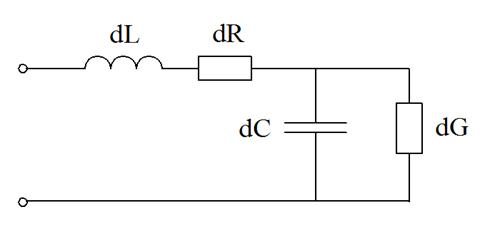
Физические свойства любого бесконечно малого отрезка линии передач характеризуются индуктивностью dL (любой отрезок проводника обладает индуктивностью), продольным реактивным сопротивлением dR (отрезок проводника обладает активным сопротивлением), емкостью dС (емкость между проводниками образующими длинную линию) и поперечной активной проводимостью dG (характеризует потери в диэлектрике линии передачи, потери на излучение и т.д.), рис.9.3а.
Если эти параметры распределены равномерно вдоль лини передачи, то линия называется однородной. Для сравнения параметров однородных линий используются погонные параметры – параметры характерные для единицы длины линии (L0, C0, R0, G0). Одним из основных параметров линии передачи является волновое сопротивлении линии r = (L0/C0)0.5.
Рассмотрим распространение сигнала генератора u = U0sin(wt) wt в линии длиной l0, имеющей нагрузку RН, рис. 9.3б.
В момент включения генератора t0 сопротивление нагрузки неизвестно (для сопротивления нагрузки и значения тока, который будет потребляться нагрузкой, необходимо время, равное времени распространения электромагнитной волны от генератора до нагрузки и обратно tU = 2tР = l0/VГ, где VГ – групповая скорость распространения электромагнитного колебания в линии передачи). Поэтому в течение времени 0 < t < tU в линии будет существовать электромагнитная волна, распространяющаяся от генератора к нагрузке (падающая волна). При отсутствии потерь в линии амплитуда и фаза падающей волны при всех значениях l (0 < l < l0) определяется выражением
UП = U0sin(w(t – tЗ)) = U0sin(w(t – l/VГ))= U0sin(wt – 2pfl/VГ) =
U0sin(wt – 2pl/lВ), (9.1.)
где
tЗ – время групповой задержки сигнала при прохождении в линии передачи расстояния l (tЗ = l/VГ);
Vг - групповая скорость распространения в линии передачи;
lВ – длина волны в линии передачи.
Из полученного выражения видно, что при прохождении в линии передачи расстояния l, фаза сигнала изменяется на величину V = – 2pl/lВ.
Рассмотрим два случая передачи энергии в длинной линии от генератора к нагрузке.
1. Сопротивление нагрузки равно волновому сопротивлению линии R = r. В интервале времени 0 < t < tU, на входе линии передачи информация о сопротивлении нагрузки отсутствует, ток генератора в линию передачи определяется волновым сопротивлением линии и равен IЛ = Uo/r. В момент времени t > tP колебания генератора достигают сопротивления нагрузки. При R = r мощность колебаний, поступивших в нагрузку, равна мощности колебаний поступающих в линию передачи от источника входного сигнала (ток и напряжение в линии передачи равны току и напряжению нагрузки). Отраженная волна отсутствует. Входное сопротивление нагруженной линии передачи равно r. При таком режиме работы вся мощность генератора поступает в нагрузку.
2. Сопротивление нагрузки не равно волновому сопротивлению линии. В этом случае в момент времени t = tP токи и напряжения в нагрузке не равны токам и напряжениям в линии передачи. Возникает неоднородность, которая формирует отраженную волну с амплитудой UO. Отношение комплексной амплитуды отраженной волны к комплексной амплитуде падающей волны называется коэффициентом отражения
KU = UП/ UO = (ZН - r)/(ZН + r), (9.2.)
где ZН – комплексное сопротивление нагрузки.
Отраженная волна распространяется по направлению к генератору. При этом разность фаз падающей и отраженной волн зависит от расстояния lН (lН -расстояние от нагрузки до сечения в линии передачи в котором исследуются ее параметры). Это приводит к следующей зависимости входного сопротивления линии от расстояния lН
ZВХ = (ZН + ir tg(2p lН/lВ))/(1 + (iZН tg(2p lН/lВ)/r) (9.3.)
На рис. 9.4 и рис. 9.5 приведены зависимости активной и реактивной составляющих входного сопротивления линии от расстояния до нагрузки l, при активном сопротивлении нагрузки равном 100 Ом и волновом сопротивлении линии r = 50 Ом.
а)

б)
Рис.9.3. Эквивалентная схема линии передачи

|

|
| Рис.9.4а. Зависимость активной составляющей входного сопротивления от расстояния до нагрузки при активном значении сопротивления нагрузки. Rн = 100 Ом, r = 50 Ом; lВ = const. | Рис.9.4б. Зависимость реактивной составляющей входного сопротивления от расстояния до нагрузки при комплексном значении сопротивления нагрузки. Rн = 100 Ом, r = 50 Ом; lВ = const. |
Если сопротивление нагрузки имеет комплексное значение, например Zн = 100 + 100i, то зависимости активной и реактивной составляющих входного сопротивления линии от расстояния до нагрузки lн имеют вид, показанный на рис.9.5а, 9.5б. Сравнение рис. 9.4 и рис. 9.5 показывает, что наличие реактивной составляющей сопротивления нагрузки значительно изменяет зависимость активной составляющей входного сопротивления линии от расстояния до нагрузки lн.

|

|
| Рис.9.5а. Зависимость активной составляющей входного сопротивления от расстояния до нагрузки при комплексном значении сопротивления нагрузки. Zн = 100 + 100i Ом, r = 50 Ом; lВ = const. | Рис.9.5б. Зависимость реактивной составляющей входного сопротивления от расстояния до нагрузки при комплексном значении сопротивления нагрузки. Zн = 100 + 100i Ом, r = 50 Ом; lВ = const. |
 
|
| Рис.9.6. Зависимость активной составляющей входного сопротивления от расстояния до нагрузки при Rн = 500 Ом >> r; lВ = const. | Рис.9.5б. Зависимость реактивной составляющей входного сопротивления от расстояния до нагрузки при Rн = 5 Ом << r; lВ = const. |
На рисунках 9.6 и 9.7 приведены зависимости входного сопротивления линии передачи от расстояния до нагрузки, при значениях сопротивлений нагрузки значительно отличающихся от волнового сопротивления линии (RН = 10r, рис.9.6 и RН = 0.1r, рис.9.7). Из рисунков видно, что при Rн >> r (разомкнутый отрезок длинной линии), частотные характеристики линии длиной 0.5nlВ, соответствуют частотным характеристикам колебательного контура (резонатора). При Rн << r (закороченный отрезок длинной линии), в качестве резонатора может использоваться отрезок линии длиной (2n-1)lВ.

|
|
а) б)
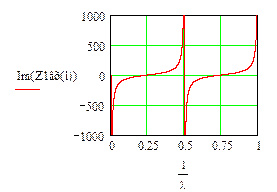
Рис. 9.8. Зависимости реактивной составляющей входного сопротивления линии от расстояния до нагрузки.
а - RН >> r; б - RН << r.
Из рисунков 9.4 и 9.5 видно, что при сопротивлении нагрузки не равном волновому сопротивлению линии, входное сопротивление линии зависит от расстояния до нагрузки и изменяется от Rн до r2/ Rн = 25 Ом. С увеличение расстояния lН, реактивная составляющая входного сопротивление периодически изменяет знак.
Из рисунков видно, что реактивная составляющая сопротивления изменяется от нуля до бесконечности при изменении длины линии на половину длины волны.
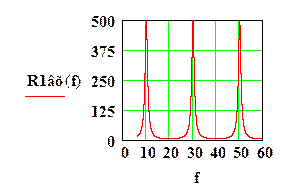
На рисунке 9.9 приведены зависимости входного сопротивления линии при RН >> r и - RН << r от частоты при постоянном значении длины линии lн = 75 мм. Из рисунка видно, что отрезки длинных линий могут быть использованы в качестве резонаторов. В отличии от характеристик резонансного контура на сосредоточенных элементах, отрезок длинной линии имеет бесконечно большое количество резонансных частот, значения которых определяются следующими выражениями:
fР = 4(2n + 1)VГР/lВ – для разомкнутого отрезка длинной линии (RН >> r);
fР = 2n VГР/lВ – для замкнутого отрезка длинной линии (RН >> r);
|

|
а) б)

|

|
в) г)
Рис.9.9. Зависимость входного сопротивления отрезка длинной линии от частоты
а- RН = 500 Ом; б - RН = 5 Ом; r = 50 Ом;
в - RН = 150 Ом; г - RН = 5 Ом; r = 15 Ом.
Поиск по сайту: