Тема: Предмет теории вероятностей

Вопрос: Монета брошена два раза. Найти вероятность того, что хотя бы один раз выпадет герб.

А) 1/4;

Б) 2/4;

В) 0,25;

*Г) 0,75;

*Д) 3/4.

Вопрос: По эмпирическому подходу вероятность события рассчитывается (статистическое определение вероятности):

А)

*Б) Как отношение числа опытов в которых событие А наступила, к общему числу исходов при проведении опытов

В) как степень уверенности наступления того и иного события.

Г) нет правильного ответа.

Вопрос: В классическом подходе вероятность события рассчитывается:

*А) Как отношение числа равновероятных благоприятных исходов наступления события А к общему числу возможных исходов

Б)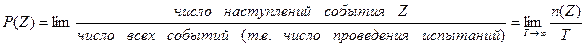

В) как степень уверенности наступления того и иного события.

Г) нет правильного ответа.

Вопрос: Какова вероятность того, что при двух подбрасываниях одной игральной кости выпадет сумма очков, равная 13?

*А) 0

Б) 1/13

В) 1/18

Г) 1/36

Вопрос: Могут ли быть противоположными события С и D, если Р(С) = 0,12; P(D) = 0,78

*А) Нет

Б) Да

Вопрос: Какие значения может принимать вероятность?

А) (-1;1)

*Б) [0;1]

В) (0;1)

Г) [-1;1]

Вопрос: Пространство элементарных событий – это...

А) любое действие, которое приводит к определенному набору результатов.

Б) конкретные результаты испытаний или их сочетание.

*В) множество всех возможных результатов эксперимента

Вопрос: Два события называются несовместными, если:

А) вероятность появления каждого из них не зависит от того, появилось другое событие или нет.

*Б) появление одного из них исключает появление другого в одном и том же испытании.

В) при рассмотрении группы событий может произойти только одно из них, а никакие другие события, не входящие в рассматриваемую группу, произойти не могут.

Г) событие А происходит тогда и только тогда, когда происходит событие В.

Вопрос: Два события называются независимыми, если:

*А) вероятность появления каждого из них не зависит от того, появилось другое событие или нет.

Б) появление одного из них исключает появление другого в одном и том же испытании.

В) при рассмотрении группы событий может произойти только одно из них, а никакие другие события, не входящие в рассматриваемую группу, произойти не могут.

Г) событие А происходит тогда и только тогда, когда происходит событие В.

Вопрос: Монета брошена 3 раза. Пусть А, В, С — события, состояние в появлении герба соответственно в первом, втором и третьем испытаниях. Ясно, что эти события являются

А) Несовместными

*Б) Независимыми

В) Зависимыми

Г) Противоположными

Вопрос: Пр о с т р а н с т в о м э л е м е н т а р н ы х и с х о д о в называется множество, содержащее все возможные результаты данного случайного эксперимента. Элементы этого множества называют э ле ме нт а р ны м и ис х о д а м и. Отношение числа исходов, благоприятствующих появлению события А к общему числу исходов называется

*А) Вероятностью события А

Б) Траекторией события А

В) Величиной события А

Г) Показателем события А

Вопрос: Выберите неверное утверждение:

А) Событие, противоположное достоверному, является невозможным

Б) Сумма вероятностей двух противоположных событий равна единице

В) Если два события единственно возможны и несовместны, то они называются противоположными

*Г) Вероятность появления одного из противоположных событий всегда больше вероятности другого.

Вопрос: Заданы множества А = {1, 3, 4}, В = {2, 3, 1, 4}, тогда для них будет неверным утверждением

А) множество А есть подмножество множества В;

Б) множества А, В пересекаются

В) множество А не равно множеству В

*Г) А и В не имеют общих элементов

Вопрос: Подбрасывают монету. События А = { выпал герб}, В = {выпала цифра}. Тогда верным для этих событий будет утверждение

А) событие А тождественно событию В

*Б) А и В не имеют общих элементов

*В) события А и В несовместны;

*Г) А и В противоположны

Вопрос: События образуют ……….группу событий, если в результате испытаний появится хотя бы одно из них

А) Независимую

Б) Зависимую

*В) Полную

Г) Совместную

Вопрос: Брошена монета. Появление герба исключает появление надписи. События «появился герб» и «появилась надпись»

А) независимые

Б) совместные

*В) несовместные

*Г) противоположные

Вопрос: Какова вероятность приземления парашютиста в заштрихованную область

*А) 11/36

Б) 1/36

В) 1/6

Г) 1/5

Вопрос: Вероятность события A при условии, что произошло событие B, называется

А) Противоположной

Б) Несовместной

*В) Условной

Г) независимой

Вопрос: В урне 5 красных, 2 синих и 3 белых шара. Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события: C + E?

вынутый шар не синий

вынутый шар разноцветный (красно-белый)

шар с четным номером - красный или белый

+ вынутый шар либо красного цвета, либо белого

Вопрос: В урне 5 красных, 2 синих и 3 белых шара. Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события AD?

+ синий шар с четным номером

либо шар с четным номером, либо он синий

шар с четным номером и не синий

синий шар с нечетным номером

Вопрос: В урне 5 красных, 2 синих и 3 белых шара. Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события AD \ E?

синий шар с четным номером кратный трем

синий шар с четным номером кратный трем

синий шар с номером 6

+ синий шар с четным номером, но не кратным трем

Вопрос: В урне 5 красных, 2 синих и 3 белых шара. Все шары пронумерованы цифрами от 1 до 10. Из урны берется наудачу 1 шар. Пусть событие A ={шар с четным номером}, событие B ={шар с номером, кратным 3}, событие C ={шар красного цвета}, событие D ={шар синего цвета}, и, наконец, E ={шар белого цвета}. Что представляют собой следующие события A + B?

шар с четным кратным трем номером

синий шар с четным номером

шар с номером 6

+ шар с номером кратным трем или двум

Вопрос: Событие А означает, что хотя бы один из трех проверенных приборов бракованный, событие В – все три прибора стандартные. Что означает событие А+В?

А. все три прибора стандартны и бракованы

Б. среди трех стандартных приборов один бракованный

+ В. хотя бы один из трех приборов стандартный или бракованный

Г. Среди трех бракованных изделий есть стандартный

Д. среди трех стандартных приборов есть хотя бы один бракованный

Вопрос: Событие А означает, что хотя бы один из трех проверенных приборов бракованный, событие В – все три прибора стандартные. Что означает событие АВ?

А. все три прибора стандартны и бракованы

Б. среди трех стандартных приборов один бракованный

В. хотя бы один из трех приборов стандартный или бракованный

Г. Среди трех бракованных изделий есть стандартный

+Д. среди трех стандартных приборов есть хотя бы один бракованный

Вопрос: В урне 5 белых, 3 черных, 4 красных шаров. Вероятность того, что из урны вынут белый или черный шар равна

А) ¼

Б) 15/8

+ В) 2/3

Г) 5/12

Поиск по сайту: