Тема: Системы случайных величин

Вопрос: Дискретные случайные величины 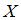и заданы законами распределения вероятностей: Тогда закон распределения вероятностей функции 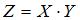имеет вид …

*

Вопрос: Двумерная дискретная случайная величина задана законом распределения вероятностей:

Тогда вероятность равна …

0,30

0,60

0,55

*0,45

Вопрос: Двумерная дискретная случайная величина задана законом распределения вероятностей:

Тогда значения a и b могут быть равны …

*

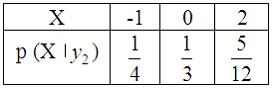
Вопрос: Двумерная дискретная случайная величина задана законом распределения вероятностей:

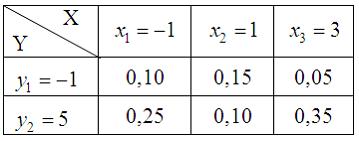
Тогда условный закон распределения вероятностей составляющей при условии, что составляющая 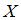приняла значение , равно …

*

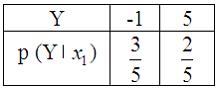
Вопрос: Двумерная дискретная случайная величина задана законом распределения вероятностей:

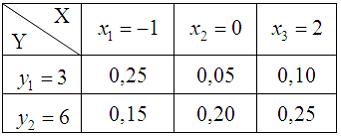
Тогда условный закон распределения вероятностей составляющей 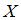при условии, что составляющая приняла значение , имеет вид …

*

Вопрос: Плотность распределения случайной величины Х, входящей в систему (Х,У) выражается через плотность распределения f(x,y) системы формулой:

*A) ;

Б) ;

В) ;

Г) .

Тема:Понятие о различных формах закона больших чисел.

Вопрос: Данное неравенство 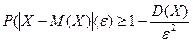выражает:

*А. неравенство Чебышева;

Б. теорему Чебышева;

В. теорему Бернулли;

Г. теорему Лапласа

Вопрос: Чтобы оценить вероятность того, что 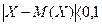, если D(X)=0,001 необходимо воспользоваться:

*А. неравенством Чебышева;

Б. теоремой Чебышева;

В. теоремой Бернулли;

Г. теоремой Лапласа

Вопрос: Данная формула выражает:

А. неравенство Чебышева;

*Б. теорему Чебышева;

В. теорему Бернулли;

Г. теорему Лапласа

Вопрос: Данная формула выражает:

А. неравенство Чебышева;

Б. теорему Чебышева;

*В. теорему Бернулли;

Г. теорему Лапласа

Вопрос: В результате проведения 200 независимых испытаний получены случайные величины с равными математическими ожиданиями и равными дисперсиями . Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания на величину, меньшую 0,5, можно оценить как …

*

Вопрос: В результате проведения 500 независимых испытаний получены случайные величины с равными математическими ожиданиями и равными дисперсиями . Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания на величину, меньшую 0,5, можно оценить как …

*

Вопрос: Вероятность выигрыша по одному лотерейному билету равна . Всего было куплено билетов. Тогда вероятность того, что количество выигравших билетов будет заключено в пределах от 15 до 25, можно оценить с использованием неравенства Чебышева как …

*

Вопрос: В результате проведения 100 независимых испытаний получены случайные величины с равными математическими ожиданиями и равными дисперсиями . Тогда вероятность того, что среднее арифметическое этих случайных величин отклонится по абсолютной величине от математического ожидания на величину, меньшую 0,5, можно оценить как …

*

Вопрос: Вероятность появления события A в каждом из 100 проведенных испытаний равна 0,8. Тогда вероятность того, что число X появлений события A будет заключена в пределах от 70 до 90, можно оценить с использованием неравенства Чебышева как …

*

Вопрос: Вероятность выигрыша по одному лотерейному билету равна 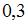. Всего было куплено билетов. Тогда вероятность того, что количество выигравших билетов будет заключено в пределах от до , можно оценить с использованием неравенства Чебышева как …

*

Вопрос: Математическое ожидание случайной величины 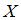равно , а дисперсия – . Тогда вероятность того, что , можно оценить с использованием неравенства Чебышева как …

*

Тема: Математическая статистика. Основные понятия и определения.

Вопрос: В результате 10 опытов получена следующая выборка: 2,2,2,3,4,4,4,5,5,5. Для неё законом распределения будет

А.

	0,3	0,1	0,3	0,5

Б.

	0,6	0,2	0,6	0,6

*В.

	0,3	0,1	0,3	0,3

Г.

	0,3	0,1	0,3	0,5

Вопрос: В результате 10 опытов получена следующая выборка: 1,1,1,3,4,4,4,5,5,5. Для неё законом распределения будет:

*А.

	0,3	0,1	0,3	0,3

Б.

	0,3	0,1	0,3	0,5

В.

	0,6	0,2	0,6	0,6

Г.

	0,3	0,1	0,3	0,5

Вопрос: В результате 10 опытов получена следующая выборка: 1,1,1,2,3,3,3,4,4,4. Для неё законом распределения будет

А.

	0,3	0,1	0,3	0,5

*Б.

	0,3	0,1	0,3	0,3

В.

	0,6	0,2	0,6	0,6

Г.

	0,3	0,1	0,3	0,5

Вопрос: В результате 10 опытов получена следующая выборка: 1,1,1,2,2,3,3,4,4,4. Для неё законом распределения будет

А.

	0,3	0,1	0,3	0,5

*Б.

	0,3	0,2	0,2	0,3

В.

	0,6	0,2	0,6	0,6

Г.

	0,3	0,1	0,3	0,5

Вопрос: Ломанную, отрезки которой соединяют точки , ,, называют:

*А. полигоном частот;

Б. полигоном относительных частот;

В. гистограмой частот;

Г. гистограммой относительных частот

Вопрос: Ломанную, отрезки которой соединяют точки , ,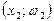, называют:

А. полигоном частот;

*Б. полигоном относительных частот;

В. гистограмой частот;

Г. гистограммой относительных частот

Вопрос: Ступенчатая фигура, состоящая из прямоугольников с основанием и высотами , называется:

А. полигоном частот;

Б. полигоном относительных частот;

*В. гистограмой частот;

гистограммой относительных частот

Вопрос: Ступенчатая фигура, состоящая из прямоугольников с основанием и высотами , называется:

А. полигоном частот;

Б. полигоном относительных частот;

В. гистограмой частот;

*Г. гистограммой относительных частот

Вопрос: Отбор, при котором объекты извлекают по одному из всей генеральной совокупности, называют:

*А. простым случайным;

Б. типическим;

В. механическим;

Г. серийным

Вопрос: Способ отбора, при котором чтобы отобрать 20% изготовленных станком деталей, отбирается каждая пятая деталь, называется:

А. простым случайным;

Б. типическим;

*В. механическим;

Г. серийным

Вопрос: Способом отбора, при котором детали изготавливаются на нескольких станках, но отбор производят не из всей совокупности деталей, изготовленных всеми станками, а из продукции каждого станка в отдельности, называется:

А. простым случайным;

*Б. типическим;

В. механическим;

Г. серийным

Вопрос: Способом отбора, при котором изделия изготавливаются большой группой станков-автоматов, а сплошному обследованию подвергается продукция только нескольких станков, называется:

А. простым случайным;

Б. типическим;

В. механическим;

*Г. серийным

Вопрос: Вариационный ряд
Из генеральной совокупности извлечена выборка объема :

Тогда относительная частота варианты равна …

0,24

*0,25

0,75

0,04

Вопрос: Мода вариационного ряда 1,1,2,2,3,3,3 равна:

А. 15

Б. 2

В. 5

*Г. 3

Вопрос: Мода вариационного ряда 1,2,2,3,4,4,4,4 равна:

А. 2

*Б. 4

В. 3

Г. 24

Вопрос: Мода вариационного ряда 1,1,1,1,2,2,4,4,4 равна:

*А. 1

Б. 3

В. 4

Г. 20

Вопрос: Мода вариационного ряда 1,1,1,1,2,3,3,3,4 равна:

*А. 1

Б. 3

В. 4

Г. 22

Вопрос: Дан вариационный ряд: 1,1,2,2,3,3,3. Найдите его медиану.

*А. 2

Б. 3

В. 4

Г. 22

Вопрос: Дан вариационный ряд: 1,2,2,3,4,4,4. Найдите его медиану.

*А. 3

Б. 1,6

В. 5,6

Г. 4

Вопрос: Дан вариационный ряд: 1,1,1,1,2,2,4,4,4. Найдите его медиану.

*2

5,4

1,2

Вопрос: Дан вариационный ряд: 1,1,1,1,2,2,4,5,5. Найдите его медиану.

*2

5,4

1,2

Вопрос: По статистическому распределению выборки

установите её объём.

*13;

39;

16;

Вопрос: По статистическому распределению выборки

установите её объём.

*10;

20;

100;

Вопрос: По статистическому распределению выборки

установите её объём.

*15;

20;

35;

Вопрос: По статистическому распределению выборки

установите её объём.

16;

26;

*10;

Вопрос: В результате некоторого эксперимента получен статистический ряд.

Тогда значение относительной частоты при будет равно…

*0,2

0,5

0,8

Вопрос: В результате некоторого эксперимента получен статистический ряд.

Тогда значение относительной частоты при будет равно…

*0,5

0,8

Вопрос: В результате некоторого эксперимента получен статистический ряд.

Тогда значение относительной частоты при будет равно…

*0,2

0,5

0,8

Вопрос: В результате некоторого эксперимента получен статистический ряд.

Тогда значение относительной частоты при будет равно…

*0,3

0,5

0,8

Вопрос: Из генеральной совокупности извлечена выборка объема n =50, полигон частот которой имеет вид

Тогда число вариант x_i =4 в выборке равно

12;

13;

14;

*15

Вопрос: Из генеральной совокупности извлечена выборка объема n =49, полигон частот которой имеет вид

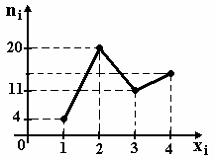
Тогда число вариант x_i =4 в выборке равно:

*14;

18;

16;

15

Вопрос: Из генеральной совокупности извлечена выборка объема n =48, полигон частот которой имеет вид

Тогда число вариант x_i =4 в выборке равно:

12;

*13;

14;

Вопрос: Из генеральной совокупности извлечена выборка объема n =47, полигон частот которой имеет вид

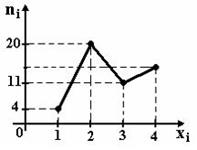
Тогда число вариант x_i =4 в выборке равно:

*12;

13;

14;

Вопрос: Дан вариационный ряд: 1,1,1,1,1,2,2,3,3,3. Найдите его выборочное среднее.

*1,8

1,2

1,6

0,8

Вопрос: Дан вариационный ряд: 1,2,2,2,3,3,4,4,4,4. Найдите его выборочное среднее.

*2,2

0,6

1,2

1,6

Вопрос: Дан вариационный ряд: 1,1,1,1,2,2,4,4,4,4. Найдите его выборочное среднее.

*2,4

0,6

1,2

1,6

Вопрос: Дан вариационный ряд: 1,1,1,1,2,2,4,4,5,5. Найдите его выборочное среднее.

*2,6

1,6

0,6

0,8

Вопрос: Статистическое распределение выборки имеет вид

Тогда значение относительной частоты 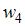равно …

0,05

0,75

*0,25

0,26

Вопрос: Из генеральной совокупности извлечена выборка объема :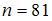

Тогда значение равно …

*34

Вопрос: Статистическое распределение выборки имеет вид

Тогда объем выборки равен …

*67

Вопрос: Полигон и гистограмма
Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид:

Тогда относительная частота варианты в выборке равна …

*0,05

0,25

0,20

0,06

Вопрос: Из генеральной совокупности извлечена выборка объема 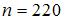, гистограмма частот которой имеет вид:

Тогда значение a равно …

*38

Вопрос: Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид:

Тогда число вариант в выборке равно …

*32

Вопрос: Из генеральной совокупности 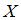извлечена выборка объема :
.
Тогда ее эмпирическая функция распределения вероятностей имеет вид …

*

Основные понятия теории множеств

Вопрос 1: Заданы множества А = {1,2,3} и B = {1,2,3,4,5}, тогда верным для них будет утверждение …

Множество А включает в себя множество В

+ Множество А есть подмножество множества В

Множества А и В не имеют общих элементов

Множества А и В равны

Вопрос 2: Заданы множества A = {1,3,5} и B = {3,1,5}, тогда верным для них будет утверждение …

+ Множество B есть подмножество множества А

+ Множество А есть подмножество множества В

Множества А и В не имеют общих элементов

+ Множества А и В равны

Вопрос 3: Заданы множества A = {1,3,5,7,8} и B = {1,5,7}, тогда верным для них будет утверждение …

+ Множество А включает в себя множество В

Множество А есть подмножество множества В

Множества А и В не имеют общих элементов

Множества А и В равны

Вопрос 4: Заданы множества A = {1,3,5} и B = {2,4,6}. Верным для них будет утверждение …

Множество А включает в себя множество В

Множество А есть подмножество множества В

+ Множества А и В не имеют общих элементов

Множества А и В равны

Вопрос 5: Пусть М – множество студентов факультета, N – множество студентов факультета, получающих стипендию. Тогда разностью M\N будет …

множество студентов факультета

множество студентов факультета, получающих стипендию

+ множество студентов факультета, не получающих стипендию

пустое множество

Вопрос 6: Пусть М – множество студентов факультета получающих стипендию, N – множество студентов факультета не получающих стипендию. Тогда объединением M U N будет …

+ множество студентов факультета

множество студентов факультета, получающих стипендию

множество студентов факультета, не получающих стипендию

пустое множество

Вопрос 7: Пусть М – множество студентов факультета получающих стипендию, N – множество студентов факультета не получающих стипендию. Тогда пересечением M и N будет …

множество студентов факультета

множество студентов факультета, получающих стипендию

множество студентов факультета, не получающих стипендию

+ пустое множество

Вопрос 8: Высказывание «Множество A не является подмножеством множества B» истинно для пары множеств …

+ A={2, 4, 6, 7}, B={4, 7}

A={6, 0, 3}, B={0, 3, 6}

A={2, 5}, B={1, 2, 5, 0}

Вопрос 9: Даны множества A={б, в, г}, B={б, в}, C={в}. Для заданных множеств будут верны утверждения, что …

множества A и B равны

+ множество C включено в множество A

множество A включено в множество C

+ множества A и B не равны

+ множество C есть подмножество множества B

Поиск по сайту: