 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема: Непрерывные случайные величины
Вопрос: Случайная величина X задана на всей оси Ох функцией распределения F (х) = 1/2 + (arctg х)/π. Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0, 1).
А) π/4
Б) 1/8
*В) 1/4
Г) 3/4
Вопрос: Случайная величина X задана плотностью распределения f(x)=x/2 в интервале (0; 6); вне этого интервала f(x)=0. Найти математическое ожидание величины X.
*А) 36
Б) 9
В) 3
Г) 0
Вопрос: Случайная величина X в интервале (—с, с) задана плотностью распределения  ; вне этого интервала f(х)=0. Найти математическое ожидание величины X.
; вне этого интервала f(х)=0. Найти математическое ожидание величины X.
*А) 0
Б) 1
В) 2с
Вопрос: Функция, определяемая по следующему правилу, называется 
А) плотность вероятности
Б) дифференциальная функция
*В) функция распределения
Г) функция надежности
Вопрос: Укажите свойства функции распределения из предложенного списка
*А) 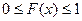
*Б) 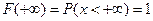
*В) 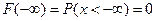
Г) F(0)=0
Вопрос: Предложенный ниже график может быть 
А) полигоном
Б) гистограммой
*В) графиком функции распределения
Г) графиком плотности вероятности
Вопрос: Предложенный ниже график может быть 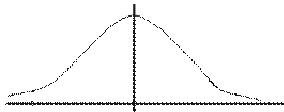
А) полигоном
Б) гистограммой
В) графиком функции распределения
*Г) графиком плотности вероятности
Вопрос: Укажите верные утверждения
*А) Функция распределения всегда неотрицательна
*Б) Функция распределения всегда неубывающая
В) Функция распределения всегда равна 1
Г) Функция распределения всегда не имеет производной
Вопрос: Производная от функции распределения непрерывной случайной величины называется
А) Функция распределения
Б) Эмпирической функцией
В) Производной функцией
*Г) Дифференциальной функцией
*Д) Плотностью распределения
Вопрос: Вероятность события, состоящего в том, что непрерывная случайная величина примет конкретное числовое значение равно
А) принадлежащему интервалу [0,1]
Б) 1
В) 0,5
*Г) 0
Вопрос: Случайная величина  задана функцией распределения
задана функцией распределения 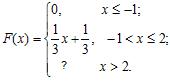 Какое значение может быть на месте пропущенного?
Какое значение может быть на месте пропущенного?
А) -1
Б) 10
В) 15
*Г) 1
Вопрос: Дисперсия непрерывной случайной величины:
А) 
Б) 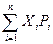
В) 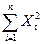
*Г) нет правильного ответа.
Вопрос: Математическое ожидание непрерывной случайной величины равно
*А) 
Б) 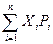
В) 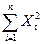
Вопрос: Функция плотности вероятностей – это…
А) функция, принимающая действительные значения на множестве событий, с помощью которой мы ставим в однозначное соответствие каждому событию некоторое число  , т.е. некоторую точку на действительной оси.
, т.е. некоторую точку на действительной оси.
*Б) функция, которая для любого интервала [Х1;Х2] на оси Х позволяет определить вероятность того что случайная переменная Х находится в этом интервале.
В) вероятность события, состоящего в том, что величина Х примет значение, меньшее х.
Вопрос: Какая из формул является функцией распределения?
А) F(x)=P(X.>x);
*Б) f(x)=F’(x);
В) F(x)= P(X=x);
*Г) F(x)=P(X<x);
Д) F(x)=f ’(x).
Вопрос: Математическое ожидание М[x] непрерывной случайной величины есть число, определяемое по формуле:
А) 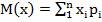 ;
;
Б) 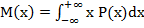 ;
;
*В) 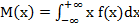 ;
;
Г) 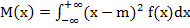 ;
;
Д)  .
.
Вопрос: Распределение вероятностей случайной величины Х задается интегральной функцией распределения:  Вычислить вероятность попадания случайной величины в интервал (2;3). Найти для случайной величины Х математическое ожидание и среднее квадратическое отклонение.
Вычислить вероятность попадания случайной величины в интервал (2;3). Найти для случайной величины Х математическое ожидание и среднее квадратическое отклонение.
*А) р=0.152, M(Х)=3, 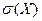 = 0.968;
= 0.968;
Б) р=0.152, M(Х)=3;
В) р=0.152, 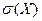 = 0.968;
= 0.968;
Г) M(Х)=3, 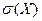 = 0.968.
= 0.968.
Вопрос: Если Х и Y- любые независимые случайные величины, a и b любые числа, то D(aХ +bY)=aD(Х)+bD(Y).
*А) Да;
Б) Нет.
Вопрос: Эксцесс случайной величины X характеризует:
*А) степень островершинности или плосковершинности распределения, т.е. степень так называемого «выпада»;
Б) степень островершинности;
В) плосковершинность распределения;
Г) степень плосковершинности.
Вопрос: Коэффициент асимметрии случайной величины X характеризует:
*А) степень асимметрии распределения относительно математического ожидания;
Б) степень островершинности или плосковершинности распределения, т.е. степень так называемого «выпада»;
В) степень островершинности;
Г) наибольшую вероятность.
Вопрос: Начальным моментом k - го порядка случайной величины X называется:
*А) математическое ожидание величины Хk, т.е. М(Хk);
Б) математическое ожидание величины (Х – М(Х)) k ;
В) математическое ожидание величины М(Х);
Г) математическое ожидание величины Х.
Вопрос: Центральным моментом k -го порядка случайной величины X называется:
А) математическое ожидание величины Хk, т.е. М(Хk);
*Б) математическое ожидание величины (Х – М(Х)) k ;
В) математическое ожидание величины Х;
Г) математическое ожидание величины М(Х).
Вопрос: Закон распределения вероятностей дискретной случайной величины 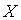 задан таблицей.
задан таблицей.
| Х | ||
| Р | 0,6 | 0,4 |
Тогда начальный момент второго порядка случайной величины X равен:
*А. 2,2
Б. 4
В. 8
Г. 1,6
Вопрос: Закон распределения вероятностей дискретной случайной величины 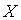 задан таблицей.
задан таблицей.
| Х | ||
| Р | 0,5 | 0,5 |
Тогда начальный момент второго порядка случайной величиныX равен:
*А. 2,5
Б. 4
В. 8
Г. 1,6
Вопрос: Закон распределения вероятностей дискретной случайной величины 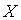 задан таблицей.
задан таблицей.
| Х | ||
| Р | 0,7 | 0,3 |
Тогда начальный момент второго порядка случайной величины X равен:
А. 2,5
Б. 4
В. 8
*Г. 1,9
Вопрос: Закон распределения вероятностей дискретной случайной величины 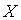 задан таблицей.
задан таблицей.
| Х | ||
| Р | 0,9 | 0,1 |
Тогда начальный момент второго порядка случайной величины X равен:
А. 4
Б. 8
В. 1,9
*Г. 1,7
Вопрос: Начальный момент 2 порядка это:
*А. 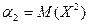
Б. 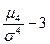
В. 
Вопрос: Асимметрия это:
А. 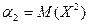
Б. 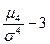
*В. 
Вопрос: Эксцесс это:
А. 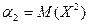
*Б. 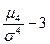
В. 
Поиск по сайту: