Тема: Статистическое определение вероятности

Вопрос: При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов.

*А) 102

Б) 100

В) 85

Г) 120

Вопрос: Отдел технического контроля обнаружил 10 нестандартных детали в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей равна

А) 0,25

*Б) 0,125

*В) 1/8

Г) 1

Вопрос: Французский ученый Бюффон провел опыт по подбрасыванию монеты, подбросив ее 4040 раз. Герб выпал в 2048 случаях. Чему равна частота события «выпадение герба»?

А) 0,54

Б) 0,569

*В) 0,5

Г) 0,6

Вопрос: По теории Менделя был проведен опыт по скрещиванию желтого гороха. Было проведено 34153 скрещивания. В 8506 случаях получился зеленый горох. Чему равна частота события «появление зеленого гороха»

А) 0,8

Б) 0,5

В) 0,3

*Г) 0,25

Тема: Теоремы сложения и умножения.

Вопрос: В урне 5 белых, 3 черных, 4 красных шаров. Вероятность того, что из урны вынут белый или черный шар равна

А) 1/4

Б) 15/8

*В) 2/3.

Г) 5/12

Вопрос: О б ъ е д и н е н и е м A ∪ B событий A и B называется событие, состоящее в том, что

*А) произошло либо A, либо B, либо оба события одновременно

Б) произошло только событие А

В) произошло только событие В

Г) оба события Аи В имеют место одновременно

Вопрос: Множество A ∪ B есть множество

*А) содержащее как элементарные исходы из множества A, так и элементарные исходы из множества B.

Б) содержащее элементарные исходы только из множества A

В) содержащее элементарные исходы только из множества B.

Г) содержащее элементарные исходы одновременно из множества A и из множества B.

Вопрос: На рисунке изображено

*А) Объединение множества А, В

Б) Пересечение множеств А, В

В) Разность множеств А.В

*Г) Сумма множеств А, В

Вопрос: На рисунке изображено

*А) пересечение множеств А,В

Б) объединение множеств А,В

В) Сумма множеств А,В

*Г) Произведение множеств А,В

Вопрос: П е р е с е ч е н и е м A ∩ B событий A и B называется

*А) событие, состоящее в том, что произошли оба события A и B одновременно.

Б) произошло либо A, либо B, либо оба события одновременно

В) произошло только событие А,

Г) произошло только событие В, А не произошло

Вопрос: События A и B называют __________, если A ∩ B = ∅.

А) Зависимыми

Б) Совместными

В) Противоположными

*Г) Несовместными

Вопрос: Что означает операция А+В?

А) событие А влечет за собой событие В

*Б) произошло хотя бы одно из двух событий А или В

В) совместное появление события А и В

Г) произошли оба события А и В

Вопрос: Два студента сдают экзамен. Если ввести события (экзамен успешно сдал первый студент) и (экзамен успешно сдал второй студент), то событие, заключающееся в том, что экзамен не сдадут оба студента, будет представлять собой выражение …

Вопрос: Два студента сдают экзамен. Если ввести события: A – экзамен успешно сдал первый студент и B – экзамен успешно сдал второй студент, то событие, заключающееся в том, что только один студент успешно сдал экзамен, будет представлять собой выражение …

Вопрос: На рисунке изображены два события A и B.

Тогда заштрихованная часть представляет собой событие …

Вопрос: Брошены монета и игральная кость. Если ввести события: A – выпал «герб» и B – появилось 5 очков, то событие, заключающееся в том, что выпала «решка» и появилось не 5 очков, будет представлять собой выражение …

Вопрос: На рисунке изображены три события A, B и C.

Тогда заштрихованная часть представляет собой событие …

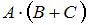
Вопрос: Имеется несколько деталей. Если ввести события: A – деталь годная и B – деталь окрашенная, то событие, заключающееся в том, что деталь негодная и окрашенная, будет представлять собой выражение …

Вопрос: Вероятность суммы двух несовместимых событий А и В равна:

А) сумме вероятности этих событий без вероятности их произведения.

Б) произведению вероятности Р этих событий.

*В) сумме вероятностей этих событий.

Вопрос: Вероятность произведения двух независимых событий А и В равна:

А) произведению вероятностей этих событий без вероятности их суммы.

*Б) произведению вероятности этих событий.

В) сумме вероятностей этих событий.

Вопрос: Суммой (объединением) нескольких случайных событий называется:

А) Событие, состоящее в появлении всех событий

*Б) Событие, состоящее в появлении хотя бы одного из этих событий

В) Событие, состоящее в появлении одного из этих событий

Вопрос: Известно, что курс евро к рублю может возрасти с вероятностью 0,55, а курс доллара к рублю может возрасти с вероятностью 0,35. Вероятность того, что возрастут оба курса, составляет 0,3. Найти вероятность того, что курс евро или доллара по отношению к рублю возрастёт.

*А) 0,6

Б) 1,2

В) 0,1

Г) 0,9

Вопрос: Петя ищет работу. Он побывал на собеседованиях в банке и страховой компании. Вероятность своего успеха в банке он оценивает в 0,5, а в страховой компании — в 0,6. Кроме того, он рассчитывает, что с вероятностью 0,3 ему поступят предложения от двух организаций сразу. Найти вероятность того, что Петя получит хотя бы одно предложение работы.

А) 1

*Б) 0,8

В) 9

Вопрос: Условие независимости события В от события А записывается в виде:

А) P(A/B)≠P(A);

Б) P(B/A) ≠P(B);

В) P(B/A) ≠P(A);

*Г) P(B/A) =P(B);

Д) P(B/A) =P(A/B)

Вопрос: В урне 6 белых шаров и 4 черных шара. Из урны дважды вынимают по одному шару, не возвращая обратно. Найти вероятность появления белого шара, при втором испытании (событие В), если при первом испытании (событие А) был извлечен черный шар.

А) 0,67

*Б) 0,27

В) 0,4

Г) 0,24

Вопрос: Если события А, В несовместны, то имеет место равенство

*А) Р(А+В)=Р(А)+Р(В)

Б) Р(А+В)=Р(А)+Р(В)-Р(АВ)

В) Р(А+В)=Р(А)Р(В)

Г) Р(А+В)=Р(А)-Р(В)

Вопрос: Если события А, В независимы, то имеет место равенство

А) Р(А*В)=Р(А)+Р(В)

Б) Р(А*В)=Р(А)+Р(В)-Р(АВ)

*В) Р(А*В)=Р(А)Р(В)

Г) Р(А*В)=Р(А)-Р(В)

Вопрос: Бросаются 2 монеты. Событие А «решетка на первой монете» и событие В «решетка на второй монете» являются:

А) Независимыми и несовместными;

В) совместными и зависимыми;

*С) независимыми и совместными;

Д) зависимыми и несовместными;

Вопрос: Событие А₁ является следствием события А₂, если:

А) появление А₁ влечет появление А₂;

В) появление А₂ не влияет на появление А₁;

С) появление А₁ не влияет на появление А₂;

*Д) нет верного утверждения;

Вопрос: В урне 5 белых и 7 черных шаров. Из урны вынимают один шар, затем второй. Найти вероятность, что оба шара будут белыми.

А) 1/25;

Б) 1/20;

В) 1/35;

Г)4/7;

*Д) 5/33

Вопрос: Вероятность хотя бы одного попадания в мишень при трех выстрелах равна 0,936. Найти вероятность попадания при одном выстреле.

А) 0,4

Б) 0,312

В) 0,064

*Г) 0,6

Тема: Формула полной вероятности. Формула Бейеса

Вопрос: Следующая формула называется

А) Формула Бернулли

Б) Формула Байеса

*В) Формула полной вероятности

Г) Неравенство Чебышева

Вопрос: Формула называется

*А) формулой Байеса

Б) формулой полной вероятности

В) Неравенством Чебышева

Г) Формулой Бернулли

Вопрос: Пусть H 1, H 2,... — полная группа событий, и A — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие H k, если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле:

*А) Байеса

Б) Полной вероятности

В) Маркова

Г) Бернулли

Вопрос: Вероятность того, что деталь попадает первому контролеру, равна 0.6, а второму – 0.4. Вероятность того, что деталь признает стандартной первый контролер, равна 0.94, второй – 0.98. Найти вероятность того, что стандартную деталь проверил первый контролер.

*А) 0,59;

Б) 0,12;

В) 0,2;

Г) 0,77.

Вопрос: Формула полной вероятности позволяет найти:

А) Вероятность события А, если известны условные вероятности гипотез при условии А

и их безусловные вероятности.

*Б) Вероятность события А, если известны условные вероятности А при условии каждой

из гипотез и вероятности этих гипотез.

В) Условные вероятности события А при условии каждой из гипотез, если известны

вероятности гипотез и их условные вероятности при условии А.

Г) Условные вероятности гипотез при условии А, если известны условные вероятности А

при условии каждой из гипотез и вероятности этих гипотез.

Д) Условные вероятности гипотез при условии А, если известны условные вероятности А

при условии каждой из гипотез и вероятность события А.

Вопрос: Формула Байеса позволяет найти:

А) Вероятность события А, если известны условные вероятности гипотез при условии А

и их безусловные вероятности.

Б) Вероятность события А, если известны условные вероятности А при условии каждой

из гипотез и вероятности этих гипотез.

В) Условные вероятности события А при условии каждой из гипотез, если известны

условные вероятности гипотез при условии А и их безусловные вероятности.

*Г) Условные вероятности гипотез при условии А, если известны условные вероятности А

при условии каждой из гипотез и вероятности этих гипотез.

Д) Условные вероятности гипотез при условии А, если известны условные вероятности А

при условии каждой из гипотез и вероятность события А.

Вопрос: При выводе формулы полной вероятности предполагается, что гипотезы:

*А) Попарно несовместны

*Б) Попарно независимы

*В) Независимы в совокупности

*Г) Образуют полную группу

*Д) В сумме дают достоверное событие

Е) В сумме дают невозможное событие

Вопрос: При выводе формулы Байеса предполагается, что гипотезы:

*А) Попарно независимы

*Б) Попарно несовместны

*В) Независимы в совокупности

*Г) Образуют полную группу

Д) В сумме дают невозможное событие

*Е) В сумме дают достоверное событие

Вопрос: О б ъ е д и н е н и е м событий A и B называется событие, состоящее в том, что

+ А) произошло либо A, либо B, либо оба события одновременно

Б) произошло только событие А

В) произошло только событие В

Г) оба события А и В имеют место одновременно

Вопрос: Множество A U B есть множество

А) содержащее как элементарные исходы из множества A, так и элементарные исходы из множества B

Б) содержащее элементарные исходы только из множества A

В) содержащее элементарные исходы только из множества B

+ Г) содержащее элементарные исходы из множества A или из множества B

Поиск по сайту: