 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Лабораторне заняття № 6
Тема: Перевірка нормальності| вибіркового розподілу
Мета|ціль| роботи: ознайомиться з|із| основними способами перевірки нормальності вибіркового розподілу при обробці експериментально одержаних|отриманих| даних.
Матеріали та устаткування|обладнання|: калькулятор, лінійка, ваги, навчальні посібники, методичний матеріал, гербарні| зразки|взірці| рослин.
Хід роботи
1. Перевірка нормальності вибіркового розподілу. Емпіричний варіаційний ряд|лава,низка| і його графік – варіаційна крива – не дозволяють з повною впевненістю стверджувати про закон розподілу сукупності з|із| зроблена узята вибірка. На величині будь-якої ознаки, що варіює позначається вплив численних|багаточисельних|, у тому числі і випадкових чинників|факторів|, що порушують чітку картину варіювання. Тим часом знання закону розподілу дозволяє уникнути можливих помилок в оцінці генеральних параметрів за вибірковими характеристиками.
При статистичному аналізі вибіркового розподілу іноді|інколи| необхідно переконатися в тому, що його форма не відрізняється від нормальної. Така перевірка пов'язана з тим, що більшість статистичних методів аналізу вибірок застосовується до нормального або близькому до нього розподілу.
Перевіряють нормальність вибіркового розподілу одним з двох способів:
1) зіставляють|співставляють| емпіричні і теоретичні частоти даної вибіркової сукупності. Відсутність істотної|суттєвої| розбіжності|розходження| між ними дає підставу|основу,заснування| вважати|лічити| розподіл таким, що не відрізняється від нормального;
2) обчислюють|обчисляють,вичисляють| показник асиметрії або ексцесу (або обох показників) і зіставляють|співставляють| їх зі|із| своєю квадратичною помилкою. Оскільки|тому що| в сукупності з|із| нормальним розподілом показники асиметрії і ексцесу рівні нулю, то перевірка нульової гіпотези в цьому випадку зводиться до оцінки істотності їх відхилення від нуля.
На цьому лабораторному занятті буде розглянутий|розгледіти| спосіб перевірки нормальності розподілу через показники асиметрії і ексцесу. Відмітити|помітити| асиметрію і ексцес можна за характером|вдачі| розподілу частот у класах варіаційного ряду|лави,низки|. Графічно асиметрія виражається|виказується,висловлюється| у вигляді скошеної варіаційної кривої, вершина якої може знаходиться|перебуває| правіше або лівіше за центр розподілу. У першому випадку асиметрія називається правобічною або позитивною, а в другому – лівобічною|лівосторонньої| або негативною|заперечної|. Разом із|поряд з,поряд із| асиметрією зустрічаються гостро-| і пласковершинні| розподіли. Крива з гострою верхівкою розподілу виникає внаслідок надмірного накопичення частот у центральних класах варіаційного ряду|лави,низки|, внаслідок|внаслідок| чого вершина варіаційної кривої виявляється|опиняється| сильно піднятою вгору|угору|. У таких випадках говорять про позитивний ексцес розподілу. Окрім|крім| одно-| зустрічаються і багатоверхівкові криві, а також пласковерхівкові| і двогорбі криві, що свідчить про наявність у|в,біля| такого розподілу негативного|заперечного| ексцесу.

| 
| 
|
| Лівобічний|лівосторонній| асиметричний розподіл | Правобічний, асиметричний розподіл | Крива із|із| зворотнім ексцесом |

| 
| |
| Крутоверхівковий розподіл (ексцес) | Двоверхівковий розподіл |
Показник асиметрії (А або g1) – є відношенням|ставленням| середньої третіх ступенів|мір| відхилень від  до куба середнього квадратичного відхилення:
до куба середнього квадратичного відхилення:
 або
або  (23)
(23)
де ε – відхилення окремих вимірювань|вимірів| від середнього арифметичного ( ).
).
Якщо в розподілі превалюють|переважають| варіанти із|із| значеннями ознаки, більшими за середню, то крива буде скошена праворуч|вправо|, а показник асиметрії буде негативним|заперечним| числом; позитивний знак характеризує лівобічну|лівосторонню| асиметрію.
Показник ексцесу (Е або g2) – чисельно рівний відношенню|ставленню| середньої четвертих ступенів|мір| відхилень від  до середнього квадратичного відхилення в четвертому ступені|мірі|
до середнього квадратичного відхилення в четвертому ступені|мірі|
 або
або  (24)
(24)
Цей показник теж|також| може мати знак плюс або мінус. Позитивний ексцес характерний|вдача| для гостроверхівкового|, негативний|заперечний| – для пласковерхівкового| і двоверхівкового розподілу. За нормального розподілу ці показники дорівнюють нулю. Насправді такий розподіл не спостерігається.
Вибіркові показники AS і EX є|з'являються,являються| випадковими величинами, які супроводжуються|супроводяться| помилками. Як критерій нормальності розподілу розраховують tAs і tEx, як відношення коефіцієнтів AS і EX до їх помилок репрезентативності, які визначають за наступними|слідуючих| наближеними формулами:
 (25)
(25)
 (26)
(26)
Точніше помилки коефіцієнтів AS і EX визначають за формулами:
 і
і  (27)
(27)
Для обчислення|підрахунку| g1 і g2 скористаємося «k-характеристиками|».
Приклад|зразок| 1. Внаслідок вимірювання|виміру| діаметру пилкових зерен у|в,біля| амфідіплоїдів| (пшениця × жито) був одержаний|отриманий| такий розподіл (табл. 22). Обробку цих даних ведуть в такій послідовності.
1. Заповнюємо табл. 22.
Таблиця 22 – Розподіл 300 пилкових зерен за діаметром
| Діаметр (у мм) | Частота (f) | Відхилення від довільного початку (а) | fa | fa2 | fa3 | fa4 |
| –3 | –84 | –756 | ||||
| –2 | –126 | –504 | ||||
| –1 | –130 | –130 | ||||
| ∑ | –259=s1 | 849=s2 | –679=s3 | 6105=s4 |
2. Розраховують суми відхилень від середньої:
першого ступеня 
другого ступеня 
третього ступеня 
четвертого ступеня 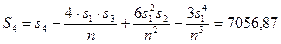
3. Обчислюють|обчисляють,вичисляють| «k-характеристики|»:
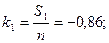



4. Після|потім| цього знаходять|находять|:


5. Квадратичні помилки  і
і  знаходять|находять| за формулами:
знаходять|находять| за формулами:


6. Перевірку істотності g1 і g2 проводять|виробляють,справляють|, обчислюючи|обчисляючи,вичисляючи|:


7. Порівнюють  і
і  з|із| табличними значення при числі ступенів свободи рівне ∞ (при рівні істотності 0,10 – 1,645; 0,05 – 1,960; 0,01 – 2,576).
з|із| табличними значення при числі ступенів свободи рівне ∞ (при рівні істотності 0,10 – 1,645; 0,05 – 1,960; 0,01 – 2,576).
У даному випадку нульова гіпотеза відкидається на рівні значущості 0,01. Отже, розподіл, що вивчається, істотно|суттєво| відрізняється від нормального; він має різко виражену|виказану,висловлену| лівобічну|лівосторонню| асиметрію і гостроверхівковість|, що виходять за межі можливих випадкових відхилень від форми, властивої нормальному розподілу.
ІІ. Практичне завдання|задавання|.
Перевірити нормальність розподілу рослин бобів кінських із|із| різною кількістю вузлів до першого бобу через показники асиметрії і ексцесу.
| Число вузлів до першого бобу | |||||||||||
| Число рослин |
ІІІ. Домашнє|хатнє| завдання|задавання|.
Перевірити нормальність розподілу рослин календули лікарської (Calendula officinalis L.) з|із| різним числом суцвіть через показники асиметрії і ексцесу.
| Варіант 1 | Варіант 2 | Варіант 3 | Варіант 4 | Варіант 5 | Варіант 6 | ||||||
| хі | f | хі | f | хі | f | хі | f | хі | f | хі | f |
Поиск по сайту: