 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Лабораторне заняття № 7
Тема: Обчислення узгодженості фактичних і теоретичних чисельностей за критерієм Пірсона.
Обчислення теоретичних чисельностей при біноміальному розподілі і розподілі Пуассона
Мета роботи: ознайомиться з алгоритмом обчислення критерію Пірсона, навчитися здійснювати перевірку на нормальність невеликих за об'ємом вибірок, а також розраховувати теоретичні частоти для біноміального розподілу і розподілу Пуассона.
Матеріали й устаткування: калькулятор, лінійка, ваги, навчальні посібники, методичний матеріал, гербарні зразки рослин.
Хід роботи
1. Обчислення критерію Пірсона (критерій χ2-квадрат або χ2-розподіл). Перевірку гіпотез про закони розподілу також проводять за допомогою спеціально розроблених критеріїв. Один з таких – критерій згоди або відповідності χ2 (запропонований в 1900 р. К. Пірсоном). Його використовують для вирішення завдань, початковими даними яких є підрахунок чисельності двох або більше вибірок, що мають 2 і більше градацій. Наприклад, ураження хворобами, розщеплювання гібридів, проростання насіння. Для обчислення критерію χ2 зіставляють різниці між фактичними чисельностями і очікуваними (обчисленими).
 (28)
(28)
де f – фактична, а m – очікувана чисельність кожного класу.
За формулою можна також розраховувати спряженість ознак, істотність причинного зв'язку між явищами за числом об'єктів, яким властива певна ознака або за кількістю і послідовністю явищ. Наприклад, можна встановити зв'язок між кольором очей і волосся, ефективністю щеплення за числом хворих і здорових людей, закономірності в спадковості ознак. Критерій χ2 часто використовується для порівняння емпіричного розподілу з очікуваними теоретичними і встановлення факту, до якого ж типу розподілів відноситься той розподіл, що вивчається – нормальному, біноміальному або Пуассона.
Чим менше розбіжність між f і m, тобто чим ближче один до одного емпіричні і очікувані чисельності, тим менше величина χ2. І навпаки, χ2 збільшується у міру збільшення різниці (f–m). Ці різниці можуть бути викликані випадковими причинами або можуть відображати реально існуючу відмінність між емпіричними і теоретичними розподілами. Для вирішення цієї альтернативи (випадкове або істотне) розраховане значення χ2 порівнюють з його значенням у додатку 2. Якщо виходить у досліді значення χ2 менше, ніж у табл. додатку 2, то нульова гіпотеза про відповідність між двома рядами чисельностей не відкидається на обраному рівні імовірності. Перевищення фактичного χ2 над табличним дає підставу визнати істотним відмінність між фактичним і очікуваним.
Число мір свободи визначається залежно від характеру аналізу і числа груп, що вивчаються. Якщо позначити через r число рядків, а через с число стовпців аналітичної таблиці, то в загальному вигляді число мір свободи дорівнюватиме (r–1)(с–1).
Приклад 1. У одному з дослідів по дослідженню спадковості у томатів було виявлено 3629 червоних і 1176 жовтих плодів. Теоретичне ж співвідношення ознак мало б бути 3:1. Чи виконується воно? Обчислимо загальну кількість плодів та їх теоретичний розподіл: 3629+1176=4805. З них повинно бути червоних  , а жовтих
, а жовтих  .
. 
За додатком 2 знаходимо  . Отже, χ2<<
. Отже, χ2<<  і відмінність фактичного розподілу від теоретичного неістотно.
і відмінність фактичного розподілу від теоретичного неістотно.
Приклад 2. Припустимо, що є два емпіричні розподіли 5, 6, 8, 10, 6 і 9, 4, 10, 6, 6. Необхідно встановити, чи розрізняються вони? Для вирішення цього завдання групують пари, обчислюють середнє, знаходять від них відхилення, а потім χ2.
| Х1 | ||||||
| Х2 | ||||||
| Середнє |


Визначимо число мір свободи f=(5–1)(2–1)=4. За таблицею (додаток 2) 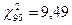 . Отже, відмінність емпіричного і теоретичного розподілів неістотна й їх можна вважати за вибірки з однієї сукупності.
. Отже, відмінність емпіричного і теоретичного розподілів неістотна й їх можна вважати за вибірки з однієї сукупності.
2. Перевірка на нормальність невеликих за об'ємом вибірок. Перевірка вибірки на нормальність розподілу може бути проведена декількома методами. Деякі з них використовуються тільки для перевірки великих вибірок, які містять більш, ніж 50 варіант. Окремі з них засновані на обчисленні асиметрії і ексцесу, суть інших методів полягає в перевірці відповідності розподілу вибіркових варіант нормальному розподілу. Наступні методи (метод середнього абсолютного відхилення, метод розмаху) застосовуються для перевірки нормальності невеликих за об'ємом вибірок.
А. Метод середнього абсолютного відхилення. Застосовується коли вибірка не перевищує 120. Алгоритм розрахунку наступний:
1. Обчислюють середнє арифметичне значення і середнє квадратичне відхилення.
2. Розраховують відхилення всіх варіант від  і обчислюють їх суму.
і обчислюють їх суму.
3. Розраховують відхилення всіх варіант від і обчислюють їх суму.
4. Обчислюють середнє абсолютне відхилення:  (29).
(29).
5. Перевіряють виконання умови 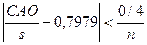 (30).
(30).
Якщо нерівність виконується, то розподіл нормальний, якщо ліва частина рівна або перевищує праву, тоді гіпотеза про нормальність розподілу вибірки відкидається.
Б. Метод розмаху. Умова: 3<n<1000. Алгоритм обчислення:
1. Знаходимо максимальний розмах у вибірці за формулою  (31).
(31).
2. Розраховують відношення розмаху до зсунутої оцінки середнього квадратичного відхилення, обчисленого за формулою  (32).
(32).
3. Співвідношення обчислюють за формулою  (33).
(33).
4. Отримане співвідношення порівнюють із стандартними мінімальним і максимальним значеннями (додаток 3а і 3б). Якщо обчислене значення знаходиться в межах між мінімальним і максимальним стандартними значеннями, гіпотеза нормального розподілу зберігається. У іншому випадку – відкидається.
3. Біноміальний розподіл. Відмічені раніше загальні закономірності в частоті появи варіант з різними значеннями ознаки, що варіює відносяться і до іншого типу розподілу, біноміального. Проте на відміну від нормального біноміальним розподілом є розподіл дискретних величин альтернативного варіювання, тобто такого варіювання, коли можливі тільки два значення ознаки, що варіює. Знаючи закономірності біноміального варіювання, можна обчислити вірогідність появи кожного з них у будь-якій незалежній вибірці з генеральної сукупності.
Теоретичний біноміальний розподіл заснований на припущенні, що поява в сукупності варіант, яким властива дана ознака, є випадковим і незалежним, і всі вони мають рівну можливість потрапити у вибірку. Співвідношення ж варіант, яким властива одна з двох альтернативних ознак, визначається біологічними закономірностями. Так, у другому поколінні гібридів (третій закон Менделя) при повному домінуванні вірогідність появи особин з домінантною ознакою – 0,75, з рецесивною – 0,25. Проте в окремих гібридів даної комбінації можуть бути й інші співвідношення домінантів і рецесивів. Побудова теоретичного біноміального розподілу і порівняння його з емпіричним дозволяють з'ясувати, чи є відхилення, що спостерігаються випадковими або вони викликані впливом якихось чинників. Теорією статистики встановлено, що відносні частоти появи в окремих вибірках з генеральної сукупності кожної з двох ознак визначаються коефіцієнтами розкладання бінома типу (p+q)k де р і q – долі кожного з двох типів у генеральній сукупності, а k – число членів вибірки. При цьому, якщо р=q=0,5, то розподіл буде симетричним; якщо р≠q – скошеним.
Для обчислення теоретичного біноміального розподілу користуються таблицею біноміальних коефіцієнтів, так званим «трикутником Паскаля ». У табл. 23 наведені коефіцієнти до k=10; кожен з них є сумою двох, що стоять справа і зліва коефіцієнтів попереднього рядка. Сума коефіцієнтів завжди дорівнює 2 в ступені k. Чисельність типів у кожній вибірці визначається множенням загального числа вибірок на відносну частоту.
Таблиця 23 – Трикутник Паскаля
| k | Біноміальні коефіцієнти | ||||||||||||||||||||
Приклад. При вивченні вибірковості запліднення кукурудзи на рильця білозерного сорту Король Філіп наносили в надлишку суміш пилку цього ж сорту і жовтозернистого сорту Воронежська 76 у співвідношенні 1:1. Після дозрівання і обмолоту від кожного з 100 качанів відібрали без вибору по 10 насінин і підрахували в кожній пробі (вибірці) кількість білих і жовтих. Отриманий при цьому розподіл вибірок за наявності в них ксенійних насінин наведено в графі 2 табл. 24.
Таблиця 24 – Емпіричний і теоретичний розподіли качанів кукурудзи за числом ксенійного насіння в незалежних вибірках по 10 насінин
| Число ксенійних насінин у вибірці | Розподіл | Накопичені частоти | |D| | ||
| емпіричний | теоретичний | емпіричний розподіл | теоретичний розподіл | ||
| - | |||||
| - | |||||
| - | - | ||||
| Сума | - | - | - |
Обчислимо теоретичні чисельності, виходячи з гіпотези, що яйцеклітинам материнського сорту не властива вибірковість і з однаковою вірогідністю можуть запліднитися пилком будь-якого з двох батьківських сортів. Для вирішення цього завдання треба провести розкладання бінома (0,5+0,5)10 і обчислити очікуване число качанів з 0, 1, 2, 3 і так далі ксенійними насіннями.
Визначаємо біноміальні коефіцієнти для k=10, що представляють відносні частоти розподілу, і проведемо розрахунки очікуваного числа качанів за схемою, округляючи (для спрощення) результати до цілих чисел:
без ксенійних насіння = 
з 1 ксеніїним сім'ям = 
з 2 ксенійнимі насінням = 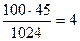 і так далі.
і так далі.

Величина критерію лямбда значно перевершує «критичне» значення (5,7>1,63), тому слід визнати даний емпіричний розподіл таким, що істотно відрізняється від теоретичного і, отже, відкинути прийняту гіпотезу про відсутність вибірковості запліднення у сорту Король Філіп.
4. Розподіл Пуассона. Коли вірогідність появи однієї з ознак альтернативного варіювання дуже мала, а другої – наближається до одиниці, біноміальний розподіл має різко виражену асиметрію. Такий розподіл рідкісних подій називають розподілом Пуассона. Прикладами такого розподілу можуть бути: кількість домішок (насіння бур'янів і т. п.) у наважці при аналізі насіння, кількість насіння, ураженого клопом-черепашкою та іншими шкідниками, наявність безпанцирних сім'янок в апробаційних зразках соняшнику, число колоній певного виду бактерій у полі зору мікроскопу і тому подібне
Приклад. У таблиці 4 наведені дані про кількість безпанцирних сім'янок соняшнику в 500 пробах сорту ВНІЇМК 6540 по 250 сім'янок в кожній (2-й рядок) (табл. 25). Розподіл Пуассона різко відрізняється від нормального, і для його опису не можуть бути використані методи, вживані для характеристики сукупностей з нормальним розподілом частот. Тому в кожному випадку дискретного розподілу частот із різко вираженою асиметрією необхідно перевірити відповідність його теоретичному розподілу Пуассона. Така перевірка проводиться шляхом зіставлення емпіричного розподілу з теоретично очікуваним для кожної 0, 1, 2 і так далі події.
Таблиця 25 – Розподіл проб із непанцирними сім'янками соняшнику
| Розподіл | Кількість непанцерних насінин у пробі | Всього | |||||||
| Фактичний | |||||||||
| Теоретично розрахований nx |
Теоретично очікуване число вибірок може, бути розраховано за формулою (34):
 (34)
(34)
де nх – очікувана чисельність вибірок з подією = 0, 1, 2 і т. д.;
N – загальне число вибірок;  – середнє число подій емпіричної сукупності;
– середнє число подій емпіричної сукупності;
х! – факторіал числа від 0 до х; е – основа натуральних логарифмів ≈ 2,718. Факторіали 0! і 1! дорівнюють одиниці.
Розрахунок теоретично очікуваних частот розподілу заснований на припущенні, що вірогідність попадання подій в кожну вибірку є постійною величиною для всієї сукупності. Техніка обчислення частот наступна. Рівняння (34) можна перетворити в  , де вираз
, де вираз  є постійним (для даного розподілу) коефіцієнтом.
є постійним (для даного розподілу) коефіцієнтом.
1. Обчислюємо 
2. 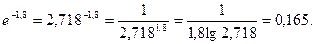
3. Знаходимо коефіцієнт 
4. Обчислюваний nх для події з округленням до цілого:
 ;
;
 ;
;
 ;
;
 ;
;
 і т.д.
і т.д.
Навіть без спеціальної перевірки можна відзначити добрий збіг фактичних і теоретичних чисельностей; це є свідоцтвом того, що розподіл числа непанцирних сім'янок у вибірках із високопанцирного сорту підпорядкований розподілу Пуассона. Випадки, коли емпіричний розподіл рідкісних подій добре узгоджується з очікуваним розподілом Пуассона, свідчать про те, що ознака, що вивчається, розподілена в сукупності, що вивчається, випадково. Слід мати на увазі, що розподіл Пуассона у міру збільшення значення х наближається до нормального і при х > 0 не відрізняється від останнього.
Поиск по сайту: