 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Рекурсивні алгоритми
| Алгоритми, що викликають самі себе, називаються рекурсивними. |
Це означає, що в тілі алгоритму є команда виклику цього алгоритму. У цьому випадку говорять про пряму рекурсію. Але буває і непряма рекурсія. Це така рекурсія, за якої, наприклад, алгоритм А викликає алгоритм В, а він, у свою чергу, викликає алгоритм С, що викликає початковий алгоритм А. Рекурсія широко застосовується в програмуванні, і це невипадково, оскільки багато математичних алгоритмів засновані на рекурсії. Вона дозволяє спростити алгоритм розв’язання завдання, значно зменшити його в розмірах. До того ж, у розв’язанні завдань перебору обійтися без рекурсії дуже складно, а часом навіть неможливо. Водночас треба знати, що для реалізації рекурсивних алгоритмів на комп’ютері треба набагато більше пам’яті, ніж нерекурсивних, тому що при кожному входженні в рекурсію змінним виділяється нова пам’ять.
Перш ніж встановити рекурсивний алгоритм, необхідно створити рекурсивний опис вихідного завдання (рекурсивну постановку завдання). Оскільки виконання рекурсивних алгоритмів здійснюється послідовним чином « занурення – вихід », то рекурсивна постановка завдання має являти собою розвинену схему, що вміщує принаймні два варіанти – під час занурення в рекурсію і під час виходу з неї, з відповідною умовою вибору необхідних дій.
Ось чому правильна постановка завдання є найважливішим моментом у використанні рекурсії для розв’язування завдань.
Обмежимося кількома прикладами алгоритмів із прямою рекурсією, а на прикладі 2 покажемо схему рекурсивного занурення і виходу алгоритму Фібоначчі.
Приклад 1. Обчислити значення функції n!
Розв’язання стає очевидним, якщо подати факторіал рекурентним співвідношенням,
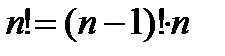
Алгоритм-функція має вигляд:
АЛГ ціл fact(ціл n)
ПОЧ ціл f
якщо n=1 або n=0
то f:=1
fact:=f
інакше f:=fact(n – 1)*n
fact:=f
Все
КІН
Поиск по сайту: