Задача про артилерійський снаряд

На заданій відстані від гармати є стіна. Відомі кут нахилу гармати і початкова швидкість снаряду. Необхідно з’ясувати, чи влучить снаряд у стіну (рис.5).

Побудуємо математичну модель розв’язання задачі. Для цього спочатку висловимо припущення, що спрощують, і допущення:

1.Снаряд вважаємо матеріальною точкою.

2.Нехтувати кривизною Землі, вважаючи її поверхню площиною.

3.Нехтуємо розмірами гармати.

4.Нехтуємо рухом Землі.

5.Вважаємо прискорення вільного падіння постійним.

6.Нехтуємо опором повітря.

З умови завдання видно, які в ній вихідні дані:

Ø 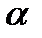- це кут під яким спрямований ствол гармати;

Ø V₀ – початкова швидкість снаряду;

Ø S – відстань до стіни;

Ø h – висота стіни.

Результатом є одне з повідомлень: «влучив» або «не влучив» снаряд у стіну.

Початкові дані підкоряються природним обмеженням:

(подумайте, як можна обгрунтувати ці обмеження).

Тепер нам треба записати мовою математики той факт, що снаряд влучив у стіну. Для цього треба знайти висоту L снаряду на відстані S від гармати: адже влучення снаряду в стіну означає, що L перебуває в межах від 0 до h. Нам треба вивести формулу для визначення L.

Ви, напевно, вже здогадалися, що маєте справу із завданням: «Рух тіла, кинутого під кутом до горизонту».

Як ви знаєте з курсу фізики, переміщення тіла, а в нашому випадку снаряду, по горизонталі і вертикалі за час t рівний, відповідно: де g – прискорення вільного падіння (9,8м/с²).

Визначимо, скільки часу знадобиться снаряду, щоб подолати відстань S:

Підставивши це значення t у вираз для у, одержимо значення L:

Звичайно, значення L, обчислене за цією формулою, може виявитися від’ємним. Це означає, що снаряд до стіни не долетить. Якщо ж L виявиться більшим від h, то снаряд перелетить через стіну.

Алгоритм має вигляд:

АЛГ Артилерійський снаряд (дійсн v, S, h, a, літ у)

АРГ v, S, h, a

РЕЗ у

ПОЧ ціл і, j

{ контроль вихідних даних }

якщо v=0

то у:=” швидкість має бути додатньою “

інакше якщо v=1000

то y:=” швидкість занадто велика “

інакше якщо S=0

то у:=” відстань має бути додатньою “

інакше якщо h=0

то у:=” висота стіни має бути додатньою “

інакше якщо а=0

то у:=” гармата не повинна стріляти в землю “

інакше якщо а=3.14/2

то у:=” гармата спрямована не у бік стіни “

інакше L:=(S*tg a – g*S²)/(2*v²*cos² a)

якщо L>h або L<0

то у:=” снаряд не влучив у стіну “

інакше у:=” снаряд влучив у стіну! “

Все

Все

Все

Все

Все

Все

Все

ДРУКУВАТИ у

КІН

Алгоритм дуже простий. Результат обчислюється за однією формулою. Однак, перш ніж він буде обчислений, ретельно аналізуються вихідні дані, і у випадку некоректності якогось із них видається відповідне повідомлення і припиняється виконання алгоритму.

При складанні програми алгоритм бажано частково видозмінити: при введенні некоректних вихідних даних програма повинна запитувати їх повторно, видаючи при цьому відповідні повідомлення.

Алгоритм мовою Паскаль має вигляд:

Program Art_snaryad;

var v, s, h, a: real; L: real;

Begin

write (‘введіть значення v, h, s, a’);

readln (v, h, s, a);

if v<=0

then writeln (‘ від’ємна швидкість неможлива ‘);

else if v>=1000

then writeln (‘ швидкість занадто велика ‘);

else if a<=0

then writeln (‘ відстань від’ємна неможлива ‘);

else if h<=0

then writeln (‘ висота стіни має бути додатньою ‘);

else if a<=0

then writeln (‘ гармата не повинна стріляти в землю ‘);

Поиск по сайту: